X 2 2x 3
renascent
Sep 18, 2025 · 6 min read
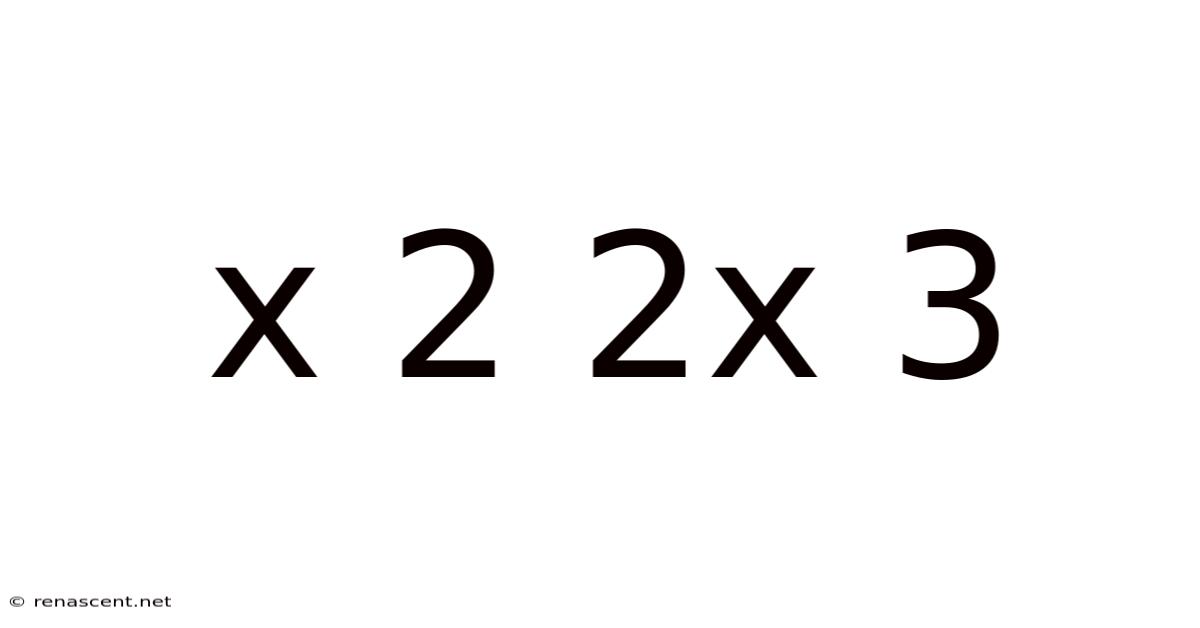
Table of Contents
Decoding the Mystery: Exploring the Mathematical Landscape of x² + 2x + 3
This article delves into the fascinating world of quadratic expressions, specifically focusing on the expression x² + 2x + 3. We will explore its properties, analyze its behavior, and investigate methods for solving related equations and inequalities. Understanding this seemingly simple expression unlocks a deeper understanding of fundamental algebraic concepts crucial for higher-level mathematics. This exploration will cover its graphical representation, its roots (or lack thereof), and its application in various mathematical contexts.
Understanding Quadratic Expressions
Before diving into the specifics of x² + 2x + 3, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, 'x') is 2. The general form of a quadratic expression is ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our case, a = 1, b = 2, and c = 3.
The term x² represents a square, geometrically visualized as a square with sides of length x. The term 2x can be seen as two rectangles, each with length x and width 1. Finally, the constant term 3 can be represented by three unit squares. Understanding these geometric representations can provide valuable insight into the nature of quadratic expressions.
Graphical Representation: Parabolas and Their Properties
Quadratic expressions, when graphed, create parabolas. Parabolas are symmetrical U-shaped curves. The parabola of x² + 2x + 3 opens upwards because the coefficient of the x² term (a = 1) is positive. If 'a' were negative, the parabola would open downwards.
The vertex of a parabola is its turning point – the lowest point for upward-opening parabolas and the highest point for downward-opening ones. The x-coordinate of the vertex can be found using the formula -b/2a. In our expression, this is -2/(2*1) = -1. Substituting x = -1 into the expression gives us the y-coordinate: (-1)² + 2(-1) + 3 = 2. Therefore, the vertex of the parabola represented by x² + 2x + 3 is (-1, 2).
The axis of symmetry is a vertical line that divides the parabola into two mirror-image halves. Its equation is x = -b/2a, which, in this case, is x = -1. This line passes through the vertex.
The y-intercept is the point where the parabola intersects the y-axis. This occurs when x = 0. Substituting x = 0 into the expression gives us 0² + 2(0) + 3 = 3. Thus, the y-intercept is (0, 3).
Finding the Roots (or Zeros): The Discriminant
The roots, or zeros, of a quadratic expression are the values of x that make the expression equal to zero. To find these, we solve the quadratic equation x² + 2x + 3 = 0. We can attempt to factor the expression, but in this instance, it's not readily factorable using integers. This is where the quadratic formula comes into play:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values (a = 1, b = 2, c = 3), we get:
x = [-2 ± √(2² - 4 * 1 * 3)] / 2 * 1 x = [-2 ± √(-8)] / 2
Notice that the expression inside the square root (the discriminant, b² - 4ac) is negative (-8). This means that the quadratic equation x² + 2x + 3 = 0 has no real roots. The roots are complex numbers involving the imaginary unit i, where i² = -1.
The roots are:
x = [-2 + √(-8)] / 2 = -1 + i√2 x = [-2 - √(-8)] / 2 = -1 - i√2
These complex roots indicate that the parabola does not intersect the x-axis. This is consistent with the fact that the vertex of the parabola lies above the x-axis (at y = 2), and the parabola opens upwards.
Completing the Square: An Alternative Approach
Completing the square is another method for solving quadratic equations and gaining further insight into the expression. The process involves manipulating the expression to create a perfect square trinomial.
Starting with x² + 2x + 3 = 0:
- Move the constant term to the right side: x² + 2x = -3
- Take half of the coefficient of x (which is 2), square it (1), and add it to both sides: x² + 2x + 1 = -3 + 1
- This creates a perfect square trinomial on the left side: (x + 1)² = -2
- Taking the square root of both sides: x + 1 = ±√(-2)
- Solving for x: x = -1 ± i√2
This confirms the complex roots we found using the quadratic formula. Completing the square also highlights the vertex form of the quadratic equation: (x - h)² + k = 0, where (h, k) represents the vertex. In our case, (x + 1)² + 2 = 0, confirming the vertex at (-1, 2).
Inequalities Involving x² + 2x + 3
We can also explore inequalities involving our quadratic expression. For example, consider the inequality x² + 2x + 3 > 0. Since the parabola opens upwards and lies entirely above the x-axis (no real roots), the inequality x² + 2x + 3 > 0 is true for all real values of x.
Conversely, the inequality x² + 2x + 3 < 0 has no real solutions because the parabola never falls below the x-axis.
Applications and Further Exploration
While the expression x² + 2x + 3 might seem abstract, it represents a fundamental building block in various mathematical applications. Understanding its properties, including its lack of real roots and its parabolic representation, is crucial for comprehending more complex mathematical concepts. These concepts underpin areas like:
- Calculus: Understanding the behavior of quadratic functions is essential for topics like optimization problems and finding derivatives and integrals.
- Physics: Quadratic equations frequently appear in physics problems involving projectile motion, where the trajectory of an object is described by a parabolic curve.
- Engineering: Many engineering designs and calculations rely on the principles of quadratic functions and their graphical representations.
- Computer Graphics: Parabolas and other quadratic curves are used extensively in computer graphics to model shapes and curves.
Frequently Asked Questions (FAQ)
-
Q: Can x² + 2x + 3 be factored using real numbers?
- A: No. The discriminant is negative, indicating no real roots, and thus it cannot be factored using real numbers.
-
Q: What is the significance of the discriminant?
- A: The discriminant (b² - 4ac) determines the nature of the roots of a quadratic equation. A positive discriminant means two distinct real roots, a zero discriminant means one real root (a repeated root), and a negative discriminant means two complex roots.
-
Q: How can I graph x² + 2x + 3?
- A: You can graph it using various methods:
- Manually: Plot points by substituting different x-values into the expression to find corresponding y-values. Use the vertex and axis of symmetry to aid in plotting.
- Using graphing software or calculator: Input the expression into a graphing tool and it will generate the parabola.
- A: You can graph it using various methods:
-
Q: Are there any practical applications of this expression?
- A: While this specific expression might not have a direct, easily-identifiable real-world application, the underlying principles of quadratic functions and their properties are widely used across various fields as previously mentioned.
Conclusion
The seemingly simple quadratic expression x² + 2x + 3 reveals a wealth of mathematical richness. From its graphical representation as a parabola to its complex roots and its application in various fields, understanding this expression provides a stepping stone to a deeper comprehension of fundamental algebraic concepts. By exploring its properties through methods like the quadratic formula and completing the square, we uncover not only the solutions to related equations but also a deeper appreciation for the elegance and power of mathematics. The journey of understanding this single expression serves as a microcosm of the larger mathematical landscape, highlighting the interconnectedness of seemingly disparate concepts and their relevance to the world around us.
Latest Posts
Latest Posts
-
Great Movie Music Composers
Sep 18, 2025
-
420 Divided By 10
Sep 18, 2025
-
Kpa To Kn M2
Sep 18, 2025
-
1000 Microliter To Ml
Sep 18, 2025
-
South America Electrical Plugs
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.