X 2 5x 1
renascent
Sep 19, 2025 · 6 min read
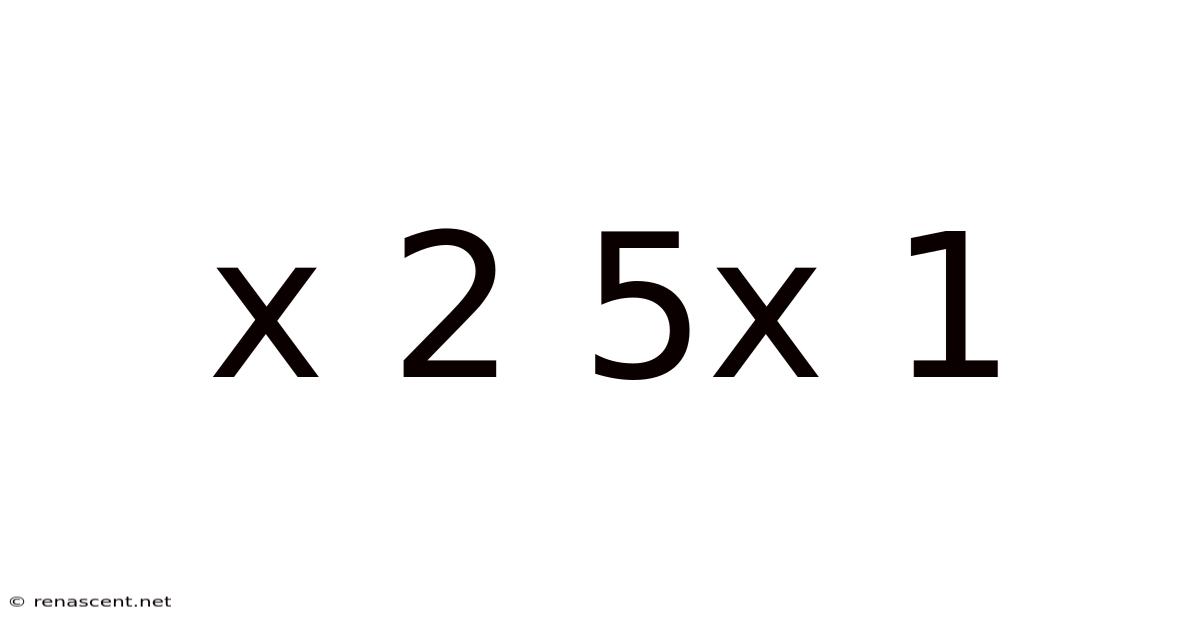
Table of Contents
Decoding x² + 5x + 1: A Deep Dive into Quadratic Equations
This article explores the quadratic equation x² + 5x + 1, examining its properties, solving methods, and real-world applications. Understanding quadratic equations is fundamental to various fields, from physics and engineering to finance and computer science. We'll break down this seemingly simple equation into its core components, revealing the rich mathematical concepts it embodies. By the end, you'll not only know how to solve this specific equation but also possess a broader understanding of quadratic equations and their significance.
Understanding the Basics: What is a Quadratic Equation?
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually 'x') is 2. It takes the general form: ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero (otherwise, it wouldn't be a quadratic equation). Our specific equation, x² + 5x + 1, fits this form with a = 1, b = 5, and c = 1.
The solutions to a quadratic equation are called roots or zeros. These are the values of 'x' that make the equation true. A quadratic equation can have two real roots, one real root (a repeated root), or two complex roots (involving imaginary numbers).
Methods for Solving Quadratic Equations: Finding the Roots of x² + 5x + 1
Several methods exist for solving quadratic equations. Let's explore the most common ones and apply them to our equation, x² + 5x + 1 = 0.
1. Factoring:
Factoring involves expressing the quadratic expression as a product of two linear expressions. Unfortunately, x² + 5x + 1 doesn't factor easily using integers. While some quadratic equations can be quickly solved by factoring, this method isn't always straightforward or even possible.
2. Completing the Square:
Completing the square is a powerful technique that transforms the quadratic equation into a perfect square trinomial, making it easier to solve. Here's how it works for x² + 5x + 1 = 0:
- Move the constant term to the right side: x² + 5x = -1
- Take half of the coefficient of x (5), square it (25/4), and add it to both sides: x² + 5x + 25/4 = -1 + 25/4
- Simplify: (x + 5/2)² = 21/4
- Take the square root of both sides: x + 5/2 = ±√(21/4)
- Solve for x: x = -5/2 ± √21/2
Therefore, the roots are x = (-5 + √21)/2 and x = (-5 - √21)/2. These are approximate values, roughly x ≈ -0.2087 and x ≈ -4.7913.
3. Quadratic Formula:
The quadratic formula is a universal solution for any quadratic equation. It provides the roots directly, regardless of whether the equation is easily factorable. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For x² + 5x + 1 = 0 (a = 1, b = 5, c = 1):
x = [-5 ± √(5² - 4 * 1 * 1)] / (2 * 1) x = [-5 ± √21] / 2
This yields the same roots as completing the square: x = (-5 + √21)/2 and x = (-5 - √21)/2.
The Discriminant: Unveiling the Nature of the Roots
The expression within the square root in the quadratic formula, b² - 4ac, is called the discriminant. It reveals valuable information about the nature of the roots:
- b² - 4ac > 0: The equation has two distinct real roots.
- b² - 4ac = 0: The equation has one real root (a repeated root).
- b² - 4ac < 0: The equation has two complex roots (involving imaginary numbers).
In our case, for x² + 5x + 1 = 0, the discriminant is 5² - 4 * 1 * 1 = 21, which is greater than 0. This confirms that the equation has two distinct real roots, as we've already calculated.
Graphical Representation: Visualizing the Quadratic Function
The equation x² + 5x + 1 = 0 can be represented graphically as a parabola. The parabola is the graph of the quadratic function y = x² + 5x + 1. The roots of the equation are the x-intercepts of the parabola – the points where the parabola intersects the x-axis (where y = 0). Visualizing the parabola helps understand the behavior of the quadratic function and the nature of its roots. The parabola opens upwards because the coefficient of x² (a = 1) is positive.
Real-World Applications: Where Do Quadratic Equations Matter?
Quadratic equations are far from abstract mathematical concepts; they have numerous practical applications:
- Physics: Calculating projectile motion (the trajectory of a ball or rocket), determining the path of a freely falling object under gravity, and modeling oscillations.
- Engineering: Designing bridges, structures, and other constructions where understanding curves and parabolic shapes is crucial.
- Finance: Modeling compound interest, determining the optimal pricing strategies, and analyzing investment returns.
- Computer Science: Used in algorithms for optimization, graphics programming, and various other computational tasks.
- Economics: Analyzing supply and demand curves, modeling economic growth, and forecasting market trends.
Expanding the Understanding: Exploring Related Concepts
Understanding x² + 5x + 1 opens doors to broader mathematical concepts:
- Polynomial Equations: Quadratic equations are a specific type of polynomial equation. Exploring higher-degree polynomial equations builds on the fundamental concepts learned here.
- Calculus: Quadratic equations form the foundation for many concepts in calculus, such as finding maxima and minima of functions.
- Linear Algebra: Matrices and linear transformations are related to solving systems of equations, including quadratic ones.
Frequently Asked Questions (FAQ)
Q: Can all quadratic equations be solved using factoring?
A: No. While factoring is a useful method for some quadratic equations, many do not factor easily using integers. The quadratic formula and completing the square are more general methods that work for all quadratic equations.
Q: What if the discriminant is negative?
A: A negative discriminant indicates that the quadratic equation has two complex roots. These roots involve imaginary numbers (involving the imaginary unit 'i', where i² = -1).
Q: What is the significance of the vertex of a parabola?
A: The vertex of a parabola represents the minimum or maximum value of the quadratic function. For a parabola that opens upwards (a > 0), the vertex represents the minimum value; for a parabola that opens downwards (a < 0), it represents the maximum value. The x-coordinate of the vertex can be found using the formula -b/2a.
Q: How can I check if my solutions are correct?
A: Substitute the calculated roots back into the original quadratic equation. If the equation holds true (both sides are equal), then your solutions are correct.
Conclusion: Mastering Quadratic Equations – One Step at a Time
The seemingly simple equation x² + 5x + 1 = 0 reveals a wealth of mathematical concepts and practical applications. By understanding the various methods for solving quadratic equations, the significance of the discriminant, and the graphical representation of the quadratic function, you've gained a strong foundation in this fundamental area of mathematics. Remember, practice is key to mastering these techniques. Continue exploring more complex equations and applications to further solidify your understanding. The world of mathematics is vast and rewarding – keep exploring!
Latest Posts
Latest Posts
-
Example Of An Srs
Sep 19, 2025
-
1 5 To A Percent
Sep 19, 2025
-
13 Divided By 5
Sep 19, 2025
-
50 Divided By 4
Sep 19, 2025
-
380 Minutes To Hours
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.