X 2 5x 6
renascent
Sep 18, 2025 · 6 min read
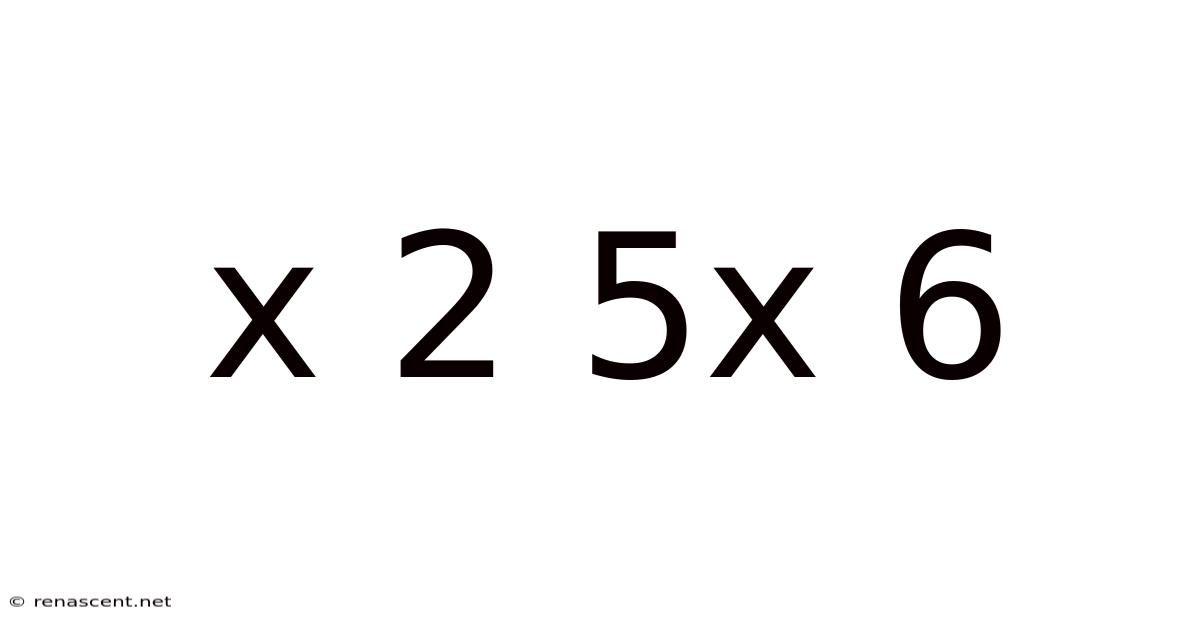
Table of Contents
Decoding the Mystery: Exploring the Mathematical Expression "x² + 5x + 6"
This article delves into the mathematical expression x² + 5x + 6, exploring its various aspects, from basic understanding to advanced applications. We'll unpack its meaning, demonstrate how to solve it using different methods, and uncover its relevance in various fields. This exploration will be beneficial for students, educators, and anyone curious about the beauty and power of algebraic expressions. Understanding quadratic equations like this is fundamental to grasping more complex mathematical concepts.
Introduction: Understanding Quadratic Equations
The expression x² + 5x + 6 is a quadratic equation. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, x) is 2. These equations are incredibly important in mathematics and have wide-ranging applications in physics, engineering, economics, and computer science. They are used to model various real-world phenomena, from projectile motion to the growth of populations. This seemingly simple expression holds a wealth of mathematical concepts within it.
Factoring the Quadratic Expression: A Step-by-Step Guide
One of the most common methods for solving a quadratic equation is through factoring. Factoring involves breaking down the expression into simpler terms that, when multiplied, give the original expression. Let's factor x² + 5x + 6:
-
Identify the coefficients: We have a coefficient of 1 for x², a coefficient of 5 for x, and a constant term of 6.
-
Find two numbers that add up to the middle coefficient (5) and multiply to the constant term (6): The numbers 2 and 3 satisfy this condition (2 + 3 = 5 and 2 * 3 = 6).
-
Rewrite the expression using these numbers: We can rewrite the expression as (x + 2)(x + 3).
-
Verification: To check our work, we can expand (x + 2)(x + 3) using the FOIL method (First, Outer, Inner, Last):
- First: x * x = x²
- Outer: x * 3 = 3x
- Inner: 2 * x = 2x
- Last: 2 * 3 = 6
Combining these terms, we get x² + 3x + 2x + 6 = x² + 5x + 6, confirming that our factoring is correct.
Therefore, the factored form of x² + 5x + 6 is (x + 2)(x + 3).
Solving for x: Finding the Roots
The factored form allows us to easily find the roots or solutions of the equation. The roots are the values of x that make the equation equal to zero. Since the product of two terms is zero, at least one of the terms must be zero. Therefore, we set each factor equal to zero and solve for x:
- x + 2 = 0 => x = -2
- x + 3 = 0 => x = -3
Thus, the roots of the quadratic equation x² + 5x + 6 are x = -2 and x = -3. These are the points where the parabola represented by the equation intersects the x-axis.
The Quadratic Formula: A More General Approach
While factoring is a useful method, it's not always applicable to all quadratic equations. The quadratic formula provides a more general solution for any quadratic equation of the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
In our case, a = 1, b = 5, and c = 6. Substituting these values into the quadratic formula:
x = [-5 ± √(5² - 4 * 1 * 6)] / (2 * 1) x = [-5 ± √(25 - 24)] / 2 x = [-5 ± √1] / 2 x = (-5 ± 1) / 2
This gives us two solutions:
- x = (-5 + 1) / 2 = -2
- x = (-5 - 1) / 2 = -3
As expected, we get the same roots as with the factoring method. The quadratic formula is a powerful tool that works even when factoring is difficult or impossible.
Graphical Representation: Visualizing the Equation
The quadratic equation x² + 5x + 6 can be represented graphically as a parabola. A parabola is a U-shaped curve. The roots of the equation (-2 and -3) represent the x-intercepts of the parabola – the points where the parabola crosses the x-axis. The parabola opens upwards because the coefficient of x² (a = 1) is positive. The vertex of the parabola, the lowest point, can be found using the formula x = -b / 2a. In this case, the x-coordinate of the vertex is -5/2, and the y-coordinate can be found by substituting this value back into the equation.
Understanding the graphical representation provides a visual understanding of the equation's behavior and its solutions.
Applications of Quadratic Equations
Quadratic equations have a wide array of applications in various fields:
-
Physics: Calculating projectile motion, the trajectory of a ball thrown in the air, relies heavily on quadratic equations.
-
Engineering: Designing bridges, buildings, and other structures often involves solving quadratic equations to determine optimal dimensions and stability.
-
Economics: Modeling supply and demand, calculating profit margins, and analyzing market trends often utilize quadratic functions.
-
Computer Science: Quadratic equations play a role in algorithm design and optimization.
-
Finance: Calculating compound interest or determining investment growth can involve quadratic equations.
Completing the Square: An Alternative Method
Another method for solving quadratic equations is completing the square. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. While potentially more complex than factoring or using the quadratic formula for simple equations, it is a crucial technique for more advanced mathematical concepts and is fundamental to understanding conic sections. The steps are as follows:
-
Move the constant term to the right side: x² + 5x = -6
-
Take half of the coefficient of x (5/2), square it (25/4), and add it to both sides: x² + 5x + 25/4 = -6 + 25/4
-
Factor the left side as a perfect square: (x + 5/2)² = 1/4
-
Take the square root of both sides: x + 5/2 = ±1/2
-
Solve for x: x = -5/2 ± 1/2, which yields x = -2 and x = -3, as before.
Frequently Asked Questions (FAQ)
-
Q: What if the quadratic equation cannot be factored easily? A: Use the quadratic formula; it works for all quadratic equations.
-
Q: What does it mean when the discriminant (b² - 4ac) is negative? A: A negative discriminant indicates that the quadratic equation has no real roots; the solutions are complex numbers involving the imaginary unit i.
-
Q: Can a quadratic equation have only one root? A: Yes, if the discriminant is equal to zero, the quadratic equation has exactly one real root (a repeated root).
-
Q: What is the relationship between the roots and the coefficients of a quadratic equation? A: For a quadratic equation ax² + bx + c = 0, the sum of the roots is -b/a, and the product of the roots is c/a. This is known as Vieta's formulas.
Conclusion: The Enduring Importance of x² + 5x + 6
The seemingly simple expression x² + 5x + 6 serves as a gateway to understanding a powerful mathematical concept: quadratic equations. Through factoring, the quadratic formula, completing the square, and graphical representation, we've explored various ways to solve and interpret this equation. Its applications extend far beyond the classroom, demonstrating the relevance of mathematics in various fields. Mastering quadratic equations is a significant step towards further mathematical explorations and successful application in many real-world scenarios. Remember, the beauty of mathematics often lies in the seemingly simple expressions that unlock a world of complex and fascinating possibilities.
Latest Posts
Latest Posts
-
Examples Of Servant Leadership
Sep 18, 2025
-
Great Movie Music Composers
Sep 18, 2025
-
420 Divided By 10
Sep 18, 2025
-
Kpa To Kn M2
Sep 18, 2025
-
1000 Microliter To Ml
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.