X 3 3x 1
renascent
Sep 21, 2025 · 6 min read
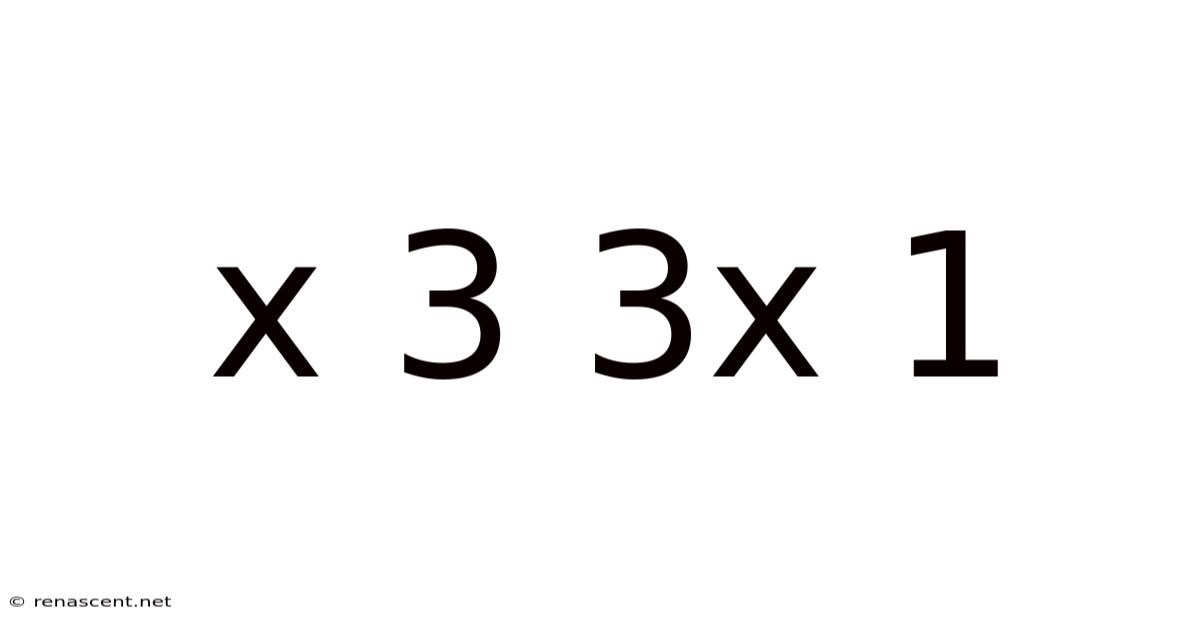
Table of Contents
Unveiling the Mystery: Exploring the Mathematical Expression "x³ + 3x² + 3x + 1"
This article delves into the fascinating mathematical expression x³ + 3x² + 3x + 1, exploring its properties, its relationship to the binomial theorem, and its applications. We'll uncover its underlying structure, learn how to factorize it, and see why it holds a significant place in algebra and calculus. Understanding this seemingly simple expression opens doors to a deeper appreciation of polynomial expansions and their real-world implications. This exploration is suitable for students learning algebra, those brushing up on their math skills, and anyone curious about the elegance of mathematical relationships.
Introduction: A Polynomial Puzzle
The expression x³ + 3x² + 3x + 1 might seem intimidating at first glance, but it’s actually a beautiful example of a perfect cubic polynomial. This means it can be neatly factored and represents a specific pattern in algebraic expansions. Understanding this pattern is key to unlocking its various applications in higher-level mathematics and even in certain scientific and engineering fields. We will break down this expression step-by-step, revealing its inherent structure and its connection to the powerful binomial theorem.
Understanding the Binomial Theorem
Before we dive into factoring x³ + 3x² + 3x + 1, let’s briefly revisit the binomial theorem. This theorem provides a formula for expanding expressions of the form (a + b)ⁿ, where 'n' is a positive integer. The general formula is:
(a + b)ⁿ = Σ (n choose k) * aⁿ⁻ᵏ * bᵏ (where k ranges from 0 to n)
The term "(n choose k)" represents the binomial coefficient, calculated as n! / (k! * (n-k)!), and denotes the number of ways to choose k items from a set of n items.
This might seem complex, but let's look at a simpler example: (a + b)³. Using the binomial theorem, we get:
(a + b)³ = (3 choose 0)a³b⁰ + (3 choose 1)a²b¹ + (3 choose 2)a¹b² + (3 choose 3)a⁰b³
Simplifying the binomial coefficients, we have:
(a + b)³ = a³ + 3a²b + 3ab² + b³
Factoring x³ + 3x² + 3x + 1: The Revelation
Now, let's relate this to our original expression, x³ + 3x² + 3x + 1. Notice the striking similarity to the expanded form of (a + b)³. If we substitute 'a' with 'x' and 'b' with '1', we get:
(x + 1)³ = x³ + 3x²(1) + 3x(1)² + 1³ = x³ + 3x² + 3x + 1
Therefore, x³ + 3x² + 3x + 1 is simply the expanded form of (x + 1)³. This factorization is incredibly significant because it simplifies the expression and allows us to easily solve equations and perform other mathematical operations.
Step-by-Step Factorization (Alternative Method)
While recognizing the binomial expansion is the quickest method, let’s also explore a step-by-step factorization approach using grouping and other algebraic techniques. This method enhances understanding of the underlying algebraic principles involved:
-
Observation: First, observe that the coefficients (1, 3, 3, 1) follow Pascal's Triangle pattern for the third row (representing the coefficients for the expansion of (a+b)³). This hints at a potential binomial cube factorization.
-
Grouping (if applicable): In some cubic polynomials, grouping terms can reveal a common factor. However, in this specific case, straightforward grouping doesn't directly lead to a factorization.
-
Trial and Error (for less obvious cases): If the binomial expansion isn't immediately apparent, you could attempt to factor it using trial and error, testing various possible factors of the constant term (1 in this case). This method becomes less efficient for higher-degree polynomials.
-
Synthetic Division (for more complex cases): For more complex cubic polynomials, synthetic division can be used to test for potential factors. This method systematically checks for potential roots of the polynomial.
In our case, the binomial expansion method is far more efficient, directly revealing the factorization (x+1)³.
Applications of x³ + 3x² + 3x + 1
This seemingly simple expression has applications in several areas:
-
Calculus: Finding the derivative and integral of x³ + 3x² + 3x + 1 is straightforward, thanks to its factored form. The derivative, representing the instantaneous rate of change, is 3x² + 6x + 3, and the integral, representing the area under the curve, is (1/4)x⁴ + x³ + (3/2)x² + x + C (where C is the constant of integration).
-
Algebraic Equations: If we set x³ + 3x² + 3x + 1 equal to zero, solving the equation becomes trivial: (x + 1)³ = 0, leading to the solution x = -1 (a triple root). Understanding this allows us to analyze the behavior of the function and find its roots.
-
Geometry and Volume: In certain geometric problems, this expression might represent a volume calculation. For instance, imagine a cube with side length (x+1). The volume of this cube will be (x+1)³, which expands to x³ + 3x² + 3x + 1.
-
Probability and Statistics (indirectly): The binomial coefficients appearing in the expansion relate to combinations and probabilities. While this specific expression doesn't directly address probability calculations, the underlying binomial theorem does play a crucial role in many probability scenarios.
Beyond the Basics: Exploring Further
The expression x³ + 3x² + 3x + 1 provides a gateway to understanding broader mathematical concepts:
-
Pascal's Triangle: The coefficients (1, 3, 3, 1) are found in Pascal's Triangle, a fascinating mathematical construct with connections to combinatorics and probability.
-
Polynomial Expansions: This expression showcases the general pattern of polynomial expansions, which are fundamental to algebra and calculus.
-
Roots of Polynomials: Understanding how to find the roots of a polynomial is crucial in many mathematical applications. The simple root of x³ + 3x² + 3x + 1 highlights the importance of factorization in this process.
Frequently Asked Questions (FAQ)
-
Q: Can this expression be factored in any other way? A: While other factorization methods exist, the most efficient and elegant way to factor x³ + 3x² + 3x + 1 is as (x + 1)³.
-
Q: What if the expression were x³ - 3x² + 3x - 1? A: That expression factors to (x - 1)³, demonstrating a similar pattern but with a negative sign.
-
Q: How do I find the derivative of x³ + 3x² + 3x + 1? A: Using the power rule of differentiation, the derivative is 3x² + 6x + 3.
-
Q: What are the applications of this in real-world scenarios? A: Although not directly apparent in everyday life, its underlying principles are used in various fields like engineering (design calculations), computer science (algorithms), and physics (modeling systems).
-
Q: Can this be applied to higher-order polynomials? A: Yes, the binomial theorem applies to any positive integer exponent 'n' allowing for similar expansions and factorizations of higher-degree polynomials.
Conclusion: A Simple Expression, Deep Insights
The seemingly simple expression x³ + 3x² + 3x + 1 reveals a wealth of mathematical richness. Its factorization as (x + 1)³ showcases the elegance and power of the binomial theorem, demonstrating a direct link between algebraic expansions and the solutions of polynomial equations. Understanding this expression not only solidifies fundamental algebraic concepts but also provides a springboard for exploring more advanced topics in calculus, geometry, and other related fields. This exploration highlights the beauty of mathematical patterns and their practical implications across various disciplines. By grasping the intricacies of this single expression, one gains a deeper appreciation for the interconnectedness of mathematical concepts and their significant role in problem-solving and understanding the world around us.
Latest Posts
Latest Posts
-
Hydrogen Bromide Lewis Structure
Sep 21, 2025
-
1 8 Of 480
Sep 21, 2025
-
4 Divided By 37
Sep 21, 2025
-
9 25 As Percentage
Sep 21, 2025
-
52 5 Kg In Lbs
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about X 3 3x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.