1/2 X 2 1/4
renascent
Sep 20, 2025 · 5 min read
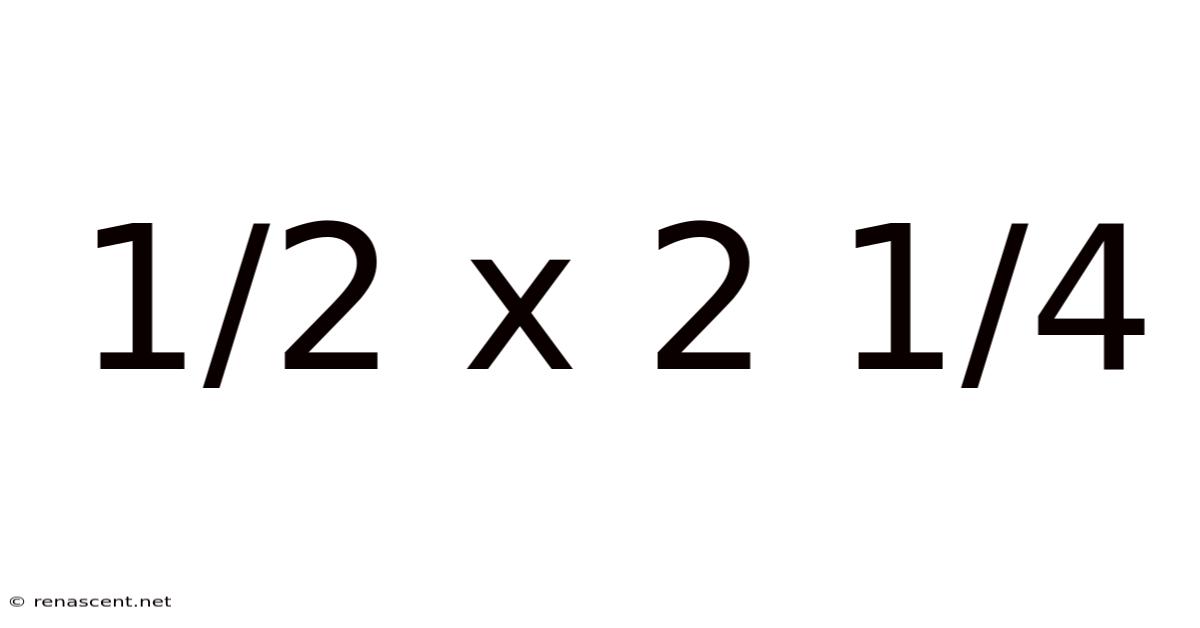
Table of Contents
Decoding 1/2 x 2 1/4: A Deep Dive into Fraction Multiplication
Understanding fraction multiplication can seem daunting at first, but with a systematic approach, it becomes a straightforward process. This article will guide you through the calculation of 1/2 x 2 1/4, explaining the steps involved, the underlying mathematical principles, and providing practical applications to solidify your understanding. We’ll also explore common misconceptions and address frequently asked questions. This comprehensive guide will leave you confident in tackling similar fraction multiplication problems.
Introduction: Why Fraction Multiplication Matters
Fraction multiplication is a fundamental concept in mathematics with wide-ranging applications in everyday life. From calculating cooking ingredients to understanding proportions in construction or finance, mastering this skill is crucial. This article focuses specifically on solving 1/2 x 2 1/4, but the principles discussed here are applicable to all fraction multiplication problems. Understanding this example will equip you to handle more complex fraction calculations with ease. We will explore different methods, from visual representations to algebraic solutions, ensuring a clear and complete understanding.
Step-by-Step Calculation of 1/2 x 2 1/4
Before we begin, remember that mixed numbers (like 2 1/4) need to be converted into improper fractions for easier multiplication. An improper fraction has a numerator larger than or equal to its denominator.
1. Convert Mixed Numbers to Improper Fractions:
-
The mixed number 2 1/4 can be converted to an improper fraction as follows:
(2 x 4) + 1 = 9. Therefore, 2 1/4 becomes 9/4.
2. Multiply the Numerators and the Denominators:
-
Now we have the problem: 1/2 x 9/4
-
Multiply the numerators (top numbers): 1 x 9 = 9
-
Multiply the denominators (bottom numbers): 2 x 4 = 8
-
This gives us the improper fraction: 9/8
3. Simplify (Reduce) the Fraction:
-
The improper fraction 9/8 can be simplified into a mixed number. We divide the numerator (9) by the denominator (8).
-
9 divided by 8 is 1 with a remainder of 1.
-
This translates to 1 1/8
Therefore, 1/2 x 2 1/4 = 1 1/8
Visualizing Fraction Multiplication
Visual aids can greatly enhance understanding, especially for those who benefit from a more concrete representation of mathematical concepts. Imagine a rectangle representing a whole unit.
-
1/2: Divide the rectangle in half. Shade one half.
-
2 1/4: Now, imagine dividing each of those halves into four equal parts (representing the 1/4 in 2 1/4). You now have eight equal parts in total. Shade two full halves and one additional quarter of a half (total 9 parts shaded).
-
Multiplication: The multiplication 1/2 x 2 1/4 represents taking one-half of 2 1/4. Looking at your visually divided rectangle, you'll see that taking one half of the shaded area leaves you with 9/8 or 1 1/8 of the original rectangle.
The Underlying Mathematical Principles
The method we used is based on the fundamental principle of fraction multiplication:
- Multiply the numerators together and multiply the denominators together. This holds true for all fraction multiplications.
This approach simplifies the calculation, making it more manageable, especially with larger or more complex fractions. The conversion to improper fractions streamlines the multiplication process, removing the need for dealing with separate whole number and fractional parts simultaneously.
Dealing with More Complex Fraction Multiplications
The principles used to solve 1/2 x 2 1/4 are applicable to any fraction multiplication problem, no matter how complex it may seem. Here’s a breakdown of how to approach more challenging situations:
-
Convert all mixed numbers to improper fractions. This is the crucial first step that simplifies the process.
-
Multiply the numerators. Straightforward multiplication of the top numbers.
-
Multiply the denominators. Straightforward multiplication of the bottom numbers.
-
Simplify the resulting fraction. This involves reducing the fraction to its lowest terms and converting any improper fractions back to mixed numbers if needed.
Common Mistakes to Avoid
-
Forgetting to Convert Mixed Numbers: One of the most common mistakes is failing to convert mixed numbers into improper fractions before multiplying. This leads to incorrect results. Always perform this conversion as the first step.
-
Incorrect Simplification: Failing to simplify the resulting fraction to its lowest terms is another frequent error. Always check if the numerator and denominator share any common factors that can be canceled out.
-
Incorrect Multiplication: Double-check your multiplication of both numerators and denominators to avoid simple arithmetic errors.
Frequently Asked Questions (FAQ)
-
Q: Why do we need to convert mixed numbers to improper fractions before multiplying?
- A: Converting to improper fractions makes the multiplication process more straightforward. Multiplying mixed numbers directly is much more complex and prone to errors. Improper fractions allow for a consistent and simpler calculation.
-
Q: What if the resulting fraction is already in its simplest form?
- A: If the resulting fraction cannot be simplified further (i.e., the numerator and denominator have no common factors other than 1), then it is already in its simplest form and no further action is required.
-
Q: Can I multiply fractions without converting to improper fractions?
- A: You can multiply mixed numbers without converting them, but it's far more complex and often involves multiple steps. Converting to improper fractions is the most efficient and recommended method.
-
Q: What if I have more than two fractions to multiply?
- A: The same principle applies. Convert all mixed numbers to improper fractions, multiply all numerators together, multiply all denominators together, and then simplify the resulting fraction.
Conclusion: Mastering Fraction Multiplication
Understanding fraction multiplication is a cornerstone of mathematical proficiency. By following the steps outlined in this article, practicing regularly, and utilizing visual aids when needed, you can master this essential skill. Remember that consistent practice is key to solidifying your understanding. Start with simpler examples and gradually progress to more complex problems. Don’t hesitate to review the steps and revisit the visual explanations as needed to reinforce your learning. With dedication and a structured approach, you’ll confidently navigate the world of fraction multiplication and its practical applications.
Latest Posts
Latest Posts
-
18 Cm In Inches
Sep 20, 2025
-
17 20 In Percent
Sep 20, 2025
-
1 12 In Decimal Form
Sep 20, 2025
-
79 5 Kg In Lbs
Sep 20, 2025
-
7 5 Mg Into Ml
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1/2 X 2 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.