120 Degrees In Radians
renascent
Sep 21, 2025 · 5 min read
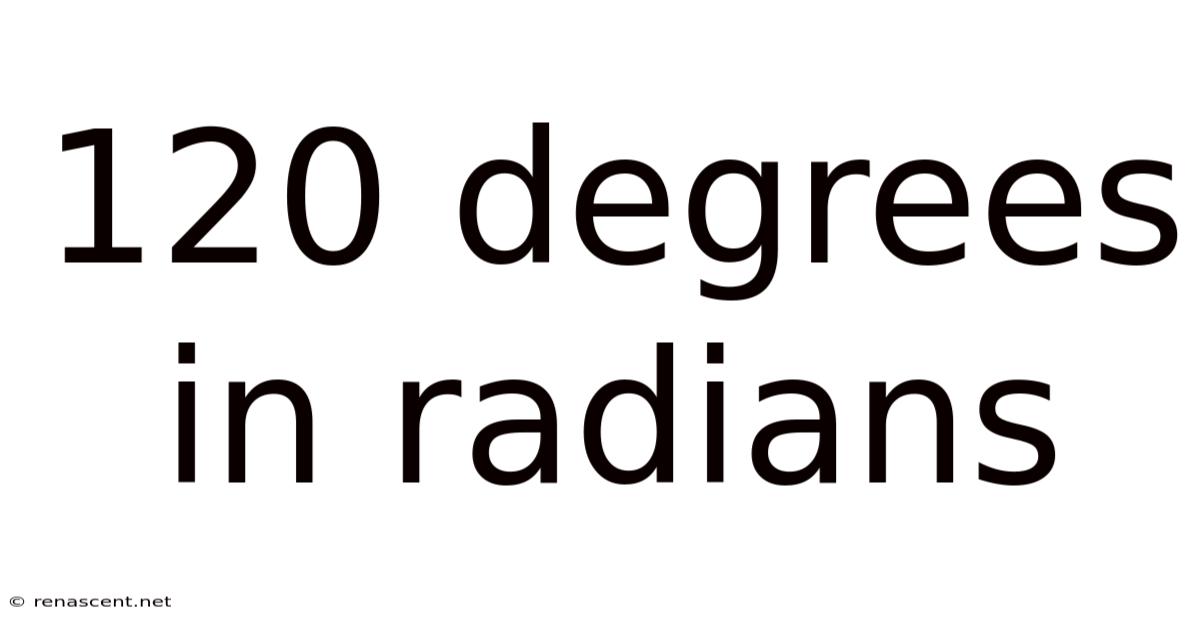
Table of Contents
120 Degrees in Radians: A Comprehensive Guide
Understanding the conversion between degrees and radians is fundamental in mathematics, particularly in trigonometry and calculus. This comprehensive guide will explore the concept of radians, explain the conversion process from degrees to radians, delve into the significance of 120 degrees in radians, and address frequently asked questions. By the end, you'll not only know how to convert 120 degrees to radians but also grasp the underlying principles and applications.
Introduction: Degrees vs. Radians
Angles are measured in two primary units: degrees and radians. Degrees, a familiar unit, divide a circle into 360 equal parts. Radians, on the other hand, are based on the radius of a circle. One radian is defined as the angle subtended at the center of a circle by an arc equal in length to the radius. This seemingly abstract definition has profound implications for simplifying many mathematical calculations.
The relationship between degrees and radians stems from the circumference of a circle. Since the circumference is 2πr (where 'r' is the radius), a complete circle (360 degrees) corresponds to an arc length of 2πr. Therefore, 360 degrees is equivalent to 2π radians. This equivalence forms the basis for all degree-to-radian conversions.
Converting Degrees to Radians: The Formula
The fundamental formula for converting degrees to radians is:
Radians = (Degrees × π) / 180
This formula arises directly from the relationship between the circumference of a circle and the radian definition. It allows us to translate any angle measured in degrees into its equivalent radian measure.
120 Degrees in Radians: A Step-by-Step Calculation
Let's apply this formula to convert 120 degrees to radians:
Radians = (120° × π) / 180°
Simplifying the fraction:
Radians = (2π) / 3
Therefore, 120 degrees is equal to (2π/3) radians. This is a crucial value often encountered in trigonometric calculations and geometric problems.
The Significance of 120 Degrees (2π/3 Radians)
The angle of 120 degrees, or (2π/3) radians, holds significant importance in several mathematical contexts:
-
Trigonometric Functions: The values of sine, cosine, and tangent at 120 degrees (or 2π/3 radians) are readily calculable and frequently used. Understanding these values is vital for solving trigonometric equations and analyzing wave functions.
-
Geometry: 120 degrees is a common angle found in various geometric shapes, such as equilateral triangles (where each interior angle is 60 degrees, and supplementary angles add up to 120 degrees), regular hexagons (interior angles of 120 degrees), and other polygons.
-
Complex Numbers: The angle plays a crucial role in representing complex numbers in polar form. Understanding the radian representation helps in operations involving complex numbers.
-
Circular Motion and Rotation: In physics, the concept of angular velocity and angular displacement is frequently expressed in radians. Therefore, an understanding of the radian measure of 120 degrees is relevant to various physics problems involving rotational motion.
Visualizing 120 Degrees (2π/3 Radians)
Imagine a circle with its center at the origin of a coordinate system. If you draw a radius from the origin to a point on the circle, and then rotate this radius counterclockwise by 120 degrees, the angle subtended at the center will be 120 degrees or (2π/3) radians. The arc length corresponding to this angle will be (2π/3) times the radius of the circle.
Beyond the Calculation: Understanding Radians' Importance
The use of radians, rather than degrees, in advanced mathematics and physics stems from their inherent connection to the radius of a circle. This relationship simplifies many formulas and calculations. For example:
-
Calculus: In calculus, many formulas involving derivatives and integrals of trigonometric functions are significantly simpler when using radians. This is because the derivative of sin(x) is cos(x) only when x is measured in radians. Using degrees requires introducing a conversion factor, making calculations more complex.
-
Physics: In many physics applications, especially those involving circular motion, rotational kinematics, or wave phenomena, radians provide a more natural and convenient unit for angular measurements. The use of radians directly relates angular displacement to arc length, simplifying the analysis of rotational motion and wave propagation.
Practical Applications of Radian Measure
The radian measure has practical applications in diverse fields beyond pure mathematics:
-
Engineering: Radians are essential in designing gears, calculating rotational speeds in machinery, and modeling oscillatory systems.
-
Computer Graphics: In computer graphics and game development, transformations, rotations, and animations rely heavily on radian measurements for accurate representation of angles and curves.
-
Signal Processing: In signal processing, analyzing waveforms and understanding phase relationships often requires the use of radians, offering a more natural way to represent the phase shift between different signals.
Frequently Asked Questions (FAQ)
Q: Why are radians preferred over degrees in higher-level mathematics?
A: Radians simplify many formulas in calculus and other advanced areas. The derivatives and integrals of trigonometric functions are much cleaner when using radians, avoiding the need for conversion factors.
Q: Can I use a calculator to convert degrees to radians?
A: Yes, most scientific calculators have a built-in function to convert between degrees and radians. Look for buttons labeled "DEG" and "RAD" or similar functions.
Q: What is the difference between a degree and a radian in terms of the angle they subtend?
A: A degree is 1/360th of a complete circle, while a radian is the angle subtended by an arc whose length is equal to the radius of the circle.
Q: What are some common radian values to memorize?
A: It's helpful to remember the radian equivalents for 0°, 30°, 45°, 60°, 90°, 180°, 270°, and 360°. These are frequently used in trigonometric calculations.
Q: Is it possible to express angles larger than 360 degrees in radians?
A: Yes, angles larger than 360 degrees simply represent multiple rotations around a circle. These can still be expressed in radians using the conversion formula.
Conclusion
Converting 120 degrees to (2π/3) radians is more than just a mathematical exercise. It reveals a deeper understanding of angles, their measurement, and their significance in various fields. Mastering this conversion is key to success in trigonometry, calculus, physics, and various engineering disciplines. The inherent relationship between radians and the radius of a circle makes it a more natural and efficient unit for advanced mathematical and scientific applications. By grasping both the mathematical process and the underlying principles, you'll be well-equipped to navigate the world of angles and their applications with confidence.
Latest Posts
Latest Posts
-
60 Divided By 10
Sep 21, 2025
-
Advantages For A Franchisor
Sep 21, 2025
-
9 10 As A Percentage
Sep 21, 2025
-
115 Kg To Lb
Sep 21, 2025
-
4 Divided By 31
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 120 Degrees In Radians . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.