16/20 As A Percentage
renascent
Sep 21, 2025 · 5 min read
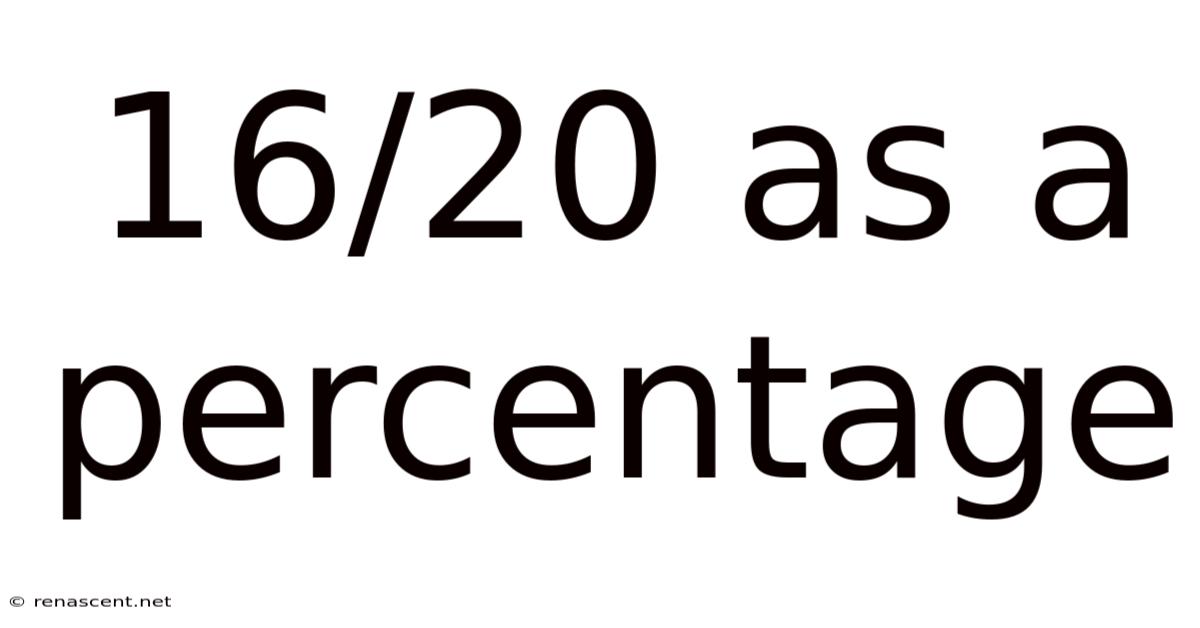
Table of Contents
Understanding 16/20 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating grades and discounts to understanding financial data and statistical analyses. This comprehensive guide will delve into the process of converting the fraction 16/20 into a percentage, exploring the underlying mathematical principles and providing practical examples to solidify your understanding. We'll also cover related concepts and frequently asked questions to offer a complete picture of this common calculation.
Introduction: Fractions, Decimals, and Percentages
Before diving into the specific conversion of 16/20, let's establish a foundational understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, 16/20 signifies 16 parts out of a total of 20 parts.
-
Decimal: A decimal is a way of expressing a fraction using a base-ten system. The decimal point separates the whole number from the fractional part. Decimals are often easier to use for calculations than fractions.
-
Percentage: A percentage expresses a fraction or decimal as a proportion of 100. The symbol "%" represents "per hundred." Percentages are commonly used to represent proportions, rates, and changes.
Calculating 16/20 as a Percentage: The Step-by-Step Approach
There are several ways to convert 16/20 to a percentage. Let's explore the most common methods:
Method 1: Direct Conversion using Division
This method involves dividing the numerator by the denominator and then multiplying the result by 100%.
-
Divide the numerator by the denominator: 16 ÷ 20 = 0.8
-
Multiply the result by 100%: 0.8 × 100% = 80%
Therefore, 16/20 is equal to 80%.
Method 2: Simplifying the Fraction First
This method involves simplifying the fraction to its lowest terms before converting to a percentage. This often makes the calculation easier.
-
Find the Greatest Common Divisor (GCD): The GCD of 16 and 20 is 4.
-
Simplify the fraction: Divide both the numerator and the denominator by the GCD: 16 ÷ 4 / 20 ÷ 4 = 4/5
-
Convert the simplified fraction to a decimal: 4 ÷ 5 = 0.8
-
Multiply the decimal by 100%: 0.8 × 100% = 80%
This method demonstrates that simplifying the fraction beforehand doesn't alter the final percentage.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the percentage.
We can set up a proportion:
16/20 = x/100
To solve for x (the percentage), we cross-multiply:
20x = 1600
x = 1600 ÷ 20
x = 80
Therefore, 16/20 is equal to 80%.
Understanding the Result: 80% Significance
Achieving an 80% score on a test or assignment is generally considered a good performance, indicating a strong grasp of the material. However, the significance of 80% depends heavily on the context. In some situations, it might be excellent, while in others, it might be considered average or even below expectations.
For instance:
-
Academic Performance: 80% on a high-school exam might be a good grade, while 80% on a university-level exam might be considered average.
-
Business Metrics: An 80% conversion rate for a marketing campaign might be extremely successful, while an 80% customer retention rate might signal areas for improvement.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is vital in many real-world situations, including:
-
Calculating Grades: Students frequently need to convert their test scores (expressed as fractions) into percentages to understand their overall performance.
-
Financial Calculations: Percentages are used extensively in finance, such as calculating interest rates, discounts, taxes, and profit margins.
-
Data Analysis: In statistics and data analysis, percentages are used to represent proportions and trends within datasets.
-
Everyday Life: Understanding percentages helps us compare prices, understand sales and discounts, and make informed decisions about purchases.
Further Exploration: Working with Different Fractions
The principles discussed above apply to converting any fraction to a percentage. Let's consider some examples:
-
Converting 3/4 to a percentage: 3 ÷ 4 = 0.75; 0.75 × 100% = 75%
-
Converting 1/2 to a percentage: 1 ÷ 2 = 0.5; 0.5 × 100% = 50%
-
Converting 7/10 to a percentage: 7 ÷ 10 = 0.7; 0.7 × 100% = 70%
These examples highlight the versatility of the conversion process.
Frequently Asked Questions (FAQ)
Q1: What if the fraction has a larger numerator than denominator?
A1: If the numerator is larger than the denominator, the resulting percentage will be greater than 100%. This indicates a value exceeding the whole. For example, 25/20 = 1.25; 1.25 × 100% = 125%.
Q2: Can I use a calculator to convert fractions to percentages?
A2: Yes, most calculators have the functionality to perform this conversion directly. Simply divide the numerator by the denominator and then multiply by 100%.
Q3: How do I handle fractions with decimals in the numerator or denominator?
A3: The process remains the same. Divide the numerator by the denominator, and then multiply by 100%. The resulting percentage may also contain a decimal.
Q4: Is there a specific formula for converting fractions to percentages?
A4: Yes, the formula is: Percentage = (Numerator / Denominator) × 100%
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a crucial skill with wide-ranging applications. Understanding the underlying mathematical principles and mastering the different methods for conversion empowers you to confidently tackle various percentage-related problems in academic, professional, and everyday contexts. Remember to practice regularly to solidify your understanding and build proficiency in this fundamental mathematical skill. The example of 16/20 equaling 80% serves as a foundational example illustrating the straightforward nature of these calculations. By applying these methods and understanding the significance of the results within different contexts, you will enhance your numeracy skills and navigate a wider range of quantitative challenges effectively.
Latest Posts
Latest Posts
-
60 Divided By 10
Sep 21, 2025
-
Advantages For A Franchisor
Sep 21, 2025
-
9 10 As A Percentage
Sep 21, 2025
-
115 Kg To Lb
Sep 21, 2025
-
4 Divided By 31
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 16/20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.