2 Sqrt 2 2
renascent
Sep 23, 2025 · 5 min read
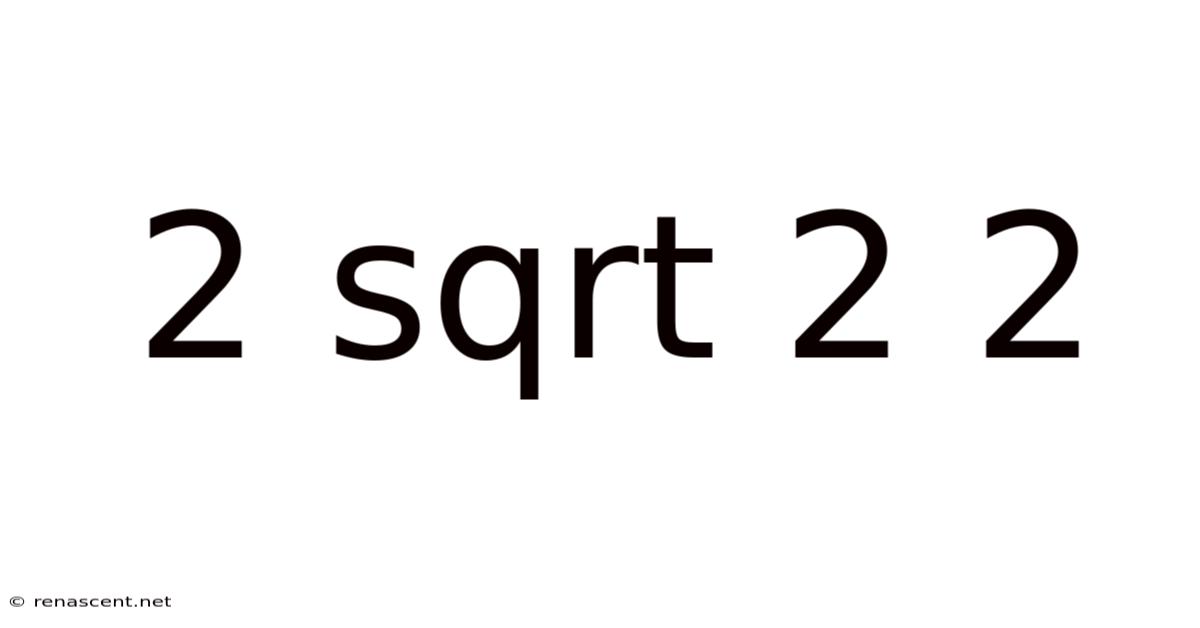
Table of Contents
Decoding 2√2: Exploring the Beauty and Significance of a Simple Expression
The expression "2√2" might seem deceptively simple at first glance. Just a few characters, yet it holds within it a rich tapestry of mathematical concepts, historical significance, and practical applications. This article delves deep into the meaning and implications of 2√2, exploring its properties, its connections to geometry, and its surprising relevance in various fields. We’ll unravel its mysteries, explaining it in a way that's accessible to everyone, regardless of their mathematical background.
Understanding the Basics: What Does 2√2 Mean?
Before we delve into the complexities, let's establish a clear understanding of what 2√2 represents. The symbol "√" denotes the square root, which is a number that, when multiplied by itself, gives the original number. Therefore, √2 is the number that, when multiplied by itself (√2 x √2), equals 2. This number is approximately 1.414. So, 2√2 simply means 2 multiplied by the square root of 2. This results in an approximate value of 2 x 1.414 = 2.828.
While seemingly straightforward, this seemingly simple expression opens doors to a deeper understanding of irrational numbers, geometrical relationships, and the elegance of mathematical principles.
The Significance of √2: An Irrational Number
The square root of 2 (√2) holds a special place in mathematics. It's classified as an irrational number, meaning it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation goes on forever without repeating, a characteristic shared by many other irrational numbers like π (pi). The discovery of the irrationality of √2 is attributed to the ancient Greek mathematicians, particularly the Pythagorean school, and it caused a significant paradigm shift in their understanding of numbers and geometry. This discovery challenged their foundational belief that all numbers could be expressed as ratios of whole numbers, leading to a deeper exploration of the nature of numbers themselves.
Geometric Representation: The Diagonal of a Square
One of the most visually appealing aspects of 2√2 lies in its geometrical representation. Consider a square with sides of length 2. According to the Pythagorean theorem (a² + b² = c²), the length of the diagonal (c) of this square can be calculated as follows:
- a = 2 (length of one side)
- b = 2 (length of the other side)
- c² = a² + b² = 2² + 2² = 4 + 4 = 8
- c = √8 = √(4 x 2) = 2√2
Therefore, the diagonal of a square with sides of length 2 has a length of 2√2. This simple geometric interpretation highlights the connection between algebra and geometry, showing how an algebraic expression can represent a tangible physical quantity. This connection is fundamental to many areas of mathematics and physics.
Applications of 2√2 in Various Fields
While seemingly abstract, the value 2√2 and its related calculations find practical applications in numerous fields:
-
Engineering and Construction: Calculations involving distances, areas, and volumes frequently utilize the Pythagorean theorem and thus incorporate square roots. In construction, for example, determining the length of diagonal bracing or the precise measurements for angled cuts often involves calculations similar to the one used for the square's diagonal.
-
Computer Graphics and Game Development: The rendering of 2D and 3D graphics relies heavily on mathematical calculations, including square roots and trigonometric functions, to accurately represent angles, distances, and positions of objects. These calculations are essential for creating realistic and immersive visual experiences.
-
Physics and Astronomy: Many physics equations involve square roots, particularly those related to motion, energy, and forces. In astronomy, calculations involving orbital mechanics and distances between celestial bodies often rely on square root calculations.
-
Electrical Engineering: In electrical circuits, calculations involving impedance, reactance, and power often involve the square root of 2. This is particularly relevant in AC (alternating current) circuits.
Deeper Mathematical Explorations: Continued Fractions and Approximations
The number 2√2 can be expressed as a continued fraction, a fascinating way to represent numbers as a nested sequence of fractions. This representation allows for increasingly accurate approximations of the value. While the details of continued fractions are beyond the scope of this introductory article, it's worth noting that such representations provide valuable insights into the nature of irrational numbers and are useful in various computational contexts.
Furthermore, approximating 2√2 using different methods, such as Taylor series expansions or numerical algorithms, is another area of mathematical exploration. The accuracy of these approximations depends on the method employed and the number of terms or iterations used.
Frequently Asked Questions (FAQ)
Q: Is 2√2 a rational or irrational number?
A: 2√2 is an irrational number. While 2 is rational, multiplying it by the irrational number √2 results in another irrational number. Irrational numbers cannot be expressed as a fraction of two integers.
Q: How can I calculate 2√2 without a calculator?
A: Precise calculation without a calculator is difficult, as √2 is irrational. However, you can find approximations. A common approximation for √2 is 1.414. Multiplying this by 2 gives approximately 2.828. More accurate approximations require more sophisticated methods.
Q: What is the difference between √2 and 2√2?
A: √2 represents the square root of 2, approximately 1.414. 2√2 represents twice the square root of 2, approximately 2.828. The difference is simply a factor of 2.
Q: Are there any other geometric interpretations of 2√2 besides the diagonal of a square?
A: Yes, 2√2 can be represented in various geometric contexts. For instance, it could represent the length of the hypotenuse of a right-angled triangle with legs of length 2 and 2, or other specific dimensions using variations of Pythagorean theorem calculations.
Conclusion: The Enduring Relevance of a Simple Expression
In conclusion, the seemingly simple expression "2√2" unveils a world of mathematical richness and practical significance. From its historical context as a cornerstone in the understanding of irrational numbers to its diverse applications across various scientific and engineering disciplines, its relevance extends far beyond its initial appearance. This exploration hopefully highlights the interconnectedness of mathematical concepts and inspires a deeper appreciation for the beauty and power hidden within even the most seemingly basic mathematical expressions. The journey from a simple algebraic expression to its geometrical representation and practical applications demonstrates the elegance and enduring relevance of mathematics in our world. Further exploration into the properties of irrational numbers, the Pythagorean theorem, and the various methods of approximation will deepen your understanding of this fascinating mathematical entity.
Latest Posts
Latest Posts
-
What Animals Eat Zooplankton
Sep 23, 2025
-
12 Divided By 40
Sep 23, 2025
-
225 Divided By 3
Sep 23, 2025
-
2 Percent Of 8
Sep 23, 2025
-
1 20 Slope Calculator
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 Sqrt 2 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.