2 X 2 10
renascent
Sep 18, 2025 · 5 min read
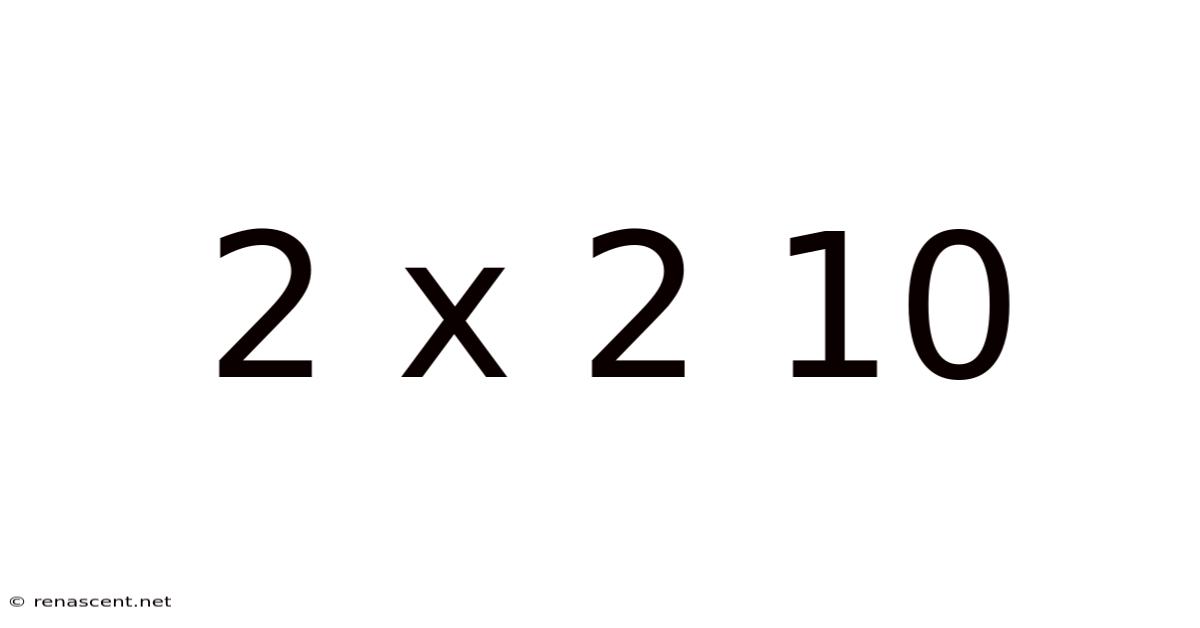
Table of Contents
Decoding "2 x 2 = 10": Exploring Non-Standard Mathematical Systems
The seemingly simple equation "2 x 2 = 10" immediately strikes us as incorrect within the familiar framework of standard arithmetic. However, this apparent falsehood opens a fascinating door to exploring non-standard mathematical systems where such an equation can hold true. This article delves into the possibilities, examining different mathematical contexts where this unconventional result becomes valid. We'll explore the concept of modular arithmetic, different number systems, and even venture into the realm of abstract algebra to illuminate the multifaceted nature of mathematical truth.
Understanding Standard Arithmetic and the Problem
In standard base-10 arithmetic, multiplication is defined as repeated addition. Therefore, 2 x 2 represents adding 2 to itself once: 2 + 2 = 4. The assertion "2 x 2 = 10" directly contradicts this fundamental principle. To understand how this equation could be true, we need to look beyond the confines of standard arithmetic.
1. Modular Arithmetic: A Different Kind of Remainder
Modular arithmetic, also known as clock arithmetic, is a system where numbers "wrap around" upon reaching a certain value, called the modulus. Imagine a 12-hour clock. If it's 11 o'clock and you add 3 hours, you don't get 14 o'clock; you get 2 o'clock. This is because the clock operates modulo 12. In modular arithmetic, we're only interested in the remainder after division by the modulus.
Let's consider a modulus of 4. In this system:
- 2 x 2 = 4
- 4 mod 4 = 0
So, in modulo 4 arithmetic, 2 x 2 is not 10. However, if we choose a different modulus, we can get closer to our target. Let's explore modulo 6:
- 2 x 2 = 4
- 4 mod 6 = 4
Still not 10. Let's try a larger modulus. Let's use modulo 8:
- 2 x 2 = 4
- 4 mod 8 = 4
This isn't working as intended. We need to consider a different approach. Instead of focusing on a simple modulo operation, we should consider the possibility of redefining the symbols themselves.
2. Redefining Symbols: A Different Number System
The statement "2 x 2 = 10" could be true if we redefine what the symbols "2" and "10" represent. Let's imagine a number system with a different base. Our standard decimal system is base-10, meaning it uses ten digits (0-9). Let's consider a hypothetical base-5 system.
In base-5, the digits are 0, 1, 2, 3, and 4. The number "10" in base-5 is equivalent to 5 in base-10. Similarly, the number "2" in base-5 remains "2" in base-10. Now let's re-evaluate "2 x 2 = 10" in this context. In base-10, this equation is false, but let's translate it into base-5:
- In base-10: 2 x 2 = 4
- In base-5: 4 (base-10) is represented as 4 (base-5).
- However, if we wanted 2 x 2 to equal 10 in a base-x system, this would mean 4 (base 10) = x + 0 (base x) = x. Therefore, the base would have to be 4. This means that we must redefine how we interpret the digit '2'.
Therefore, within a base-4 system, the equation can be interpreted as follows:
- 2 (base 4) = 2 (base 10)
- 2 x 2 = 4 (base 10)
- 4 (base 10) = 10 (base 4)
Thus, in base-4, 2 x 2 = 10 is a valid statement. This demonstrates how a change in the numerical base alters the interpretation of the equation.
3. Abstract Algebra and Group Theory
Abstract algebra provides even more avenues for interpreting unconventional equations. In group theory, we study algebraic structures with specific properties. It's possible to define operations that behave differently than standard multiplication.
Consider a group with elements {0, 1, 2, 3} and an operation denoted by *. We could define this operation such that:
- 0 * 0 = 0
- 0 * 1 = 1
- 0 * 2 = 2
- 0 * 3 = 3
- 1 * 1 = 0
- 1 * 2 = 3
- 1 * 3 = 2
- 2 * 2 = 0
- 2 * 3 = 1
- 3 * 3 = 0
In this system, we have redefined the concept of multiplication. While this specific example doesn't directly yield "2 * 2 = 10," it demonstrates the potential for constructing mathematical systems where unconventional results are valid. The key is the definition of the underlying operations.
4. Beyond Numbers: Symbolic Manipulation
We can also interpret "2 x 2 = 10" as a purely symbolic manipulation, devoid of numerical meaning. Imagine a system where "2" and "10" represent abstract entities, and "x" represents a specific operation defined within that system. The equation would then become a statement about the relationship between those entities and that specific operation, independent of our typical understanding of numbers.
5. The Importance of Context
The fundamental lesson here is the critical importance of context in mathematics. "2 x 2 = 10" is demonstrably false within the context of standard arithmetic but can be true within other mathematical frameworks. This highlights that mathematical "truth" isn't absolute but is always relative to the system within which it's defined.
Frequently Asked Questions (FAQ)
-
Q: Is "2 x 2 = 10" ever true in standard mathematics? A: No, it's unequivocally false in standard base-10 arithmetic.
-
Q: What are the practical applications of non-standard mathematical systems? A: Modular arithmetic, for instance, is crucial in cryptography, computer science (hashing algorithms), and even music theory. Other systems find applications in advanced physics and abstract computer science.
-
Q: Can any equation be made true in some mathematical system? A: While it's generally possible to construct a system where a specific equation holds true, it's not necessarily a meaningful or useful system. The usefulness of a mathematical system depends on its consistency, coherence, and applicability to real-world problems or theoretical explorations.
Conclusion
The deceptively simple equation "2 x 2 = 10" serves as a powerful reminder of the richness and flexibility of mathematics. While false within standard arithmetic, it opens up a fascinating exploration of alternative mathematical systems. From modular arithmetic to abstract algebra and even symbolic manipulation, the equation highlights that the meaning and "truth" of a mathematical statement are profoundly dependent on the context in which it's considered. Understanding these different systems not only enhances our mathematical knowledge but also deepens our appreciation for the boundless creativity and adaptability of mathematics itself. It encourages us to question assumptions, explore possibilities, and appreciate the fact that even a seemingly simple equation can lead to a deep and rewarding mathematical journey.
Latest Posts
Latest Posts
-
Estate In Fee Simple
Sep 18, 2025
-
Expanded Notation In Maths
Sep 18, 2025
-
Michael C Hall Younger
Sep 18, 2025
-
70 Mph In Km
Sep 18, 2025
-
Acrylic Powder And Liquid
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.