2 X 2 4
renascent
Sep 23, 2025 · 6 min read
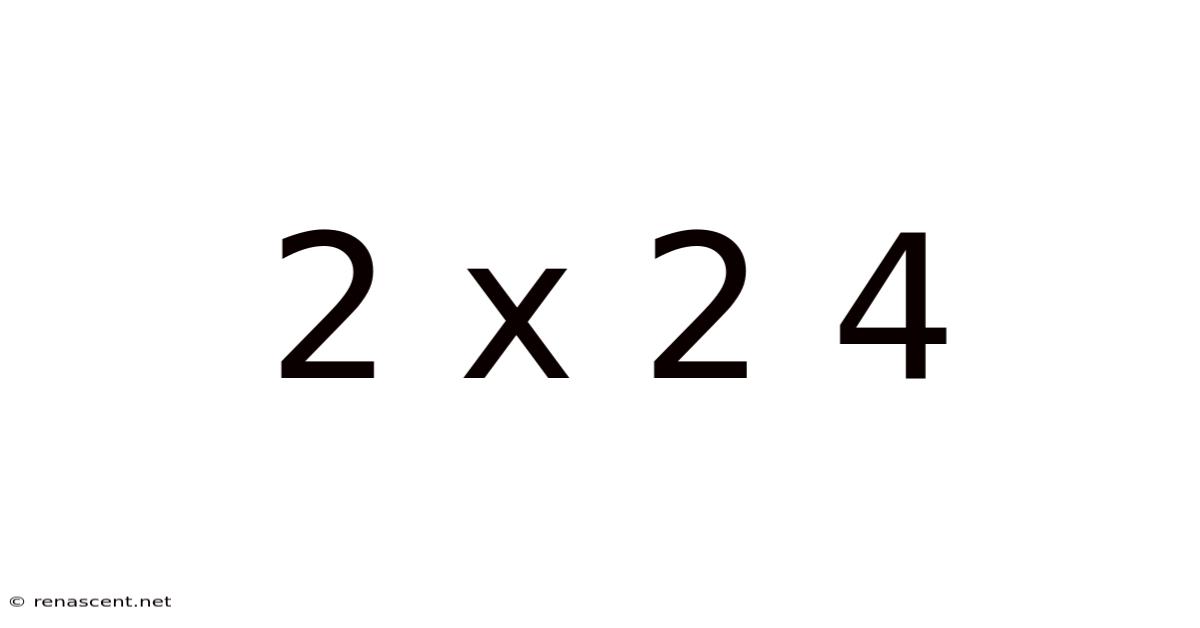
Table of Contents
Decoding 2 x 2 = 4: A Deep Dive into Multiplication and its Implications
The seemingly simple equation, 2 x 2 = 4, forms the bedrock of arithmetic and underpins countless mathematical concepts. This article will explore this fundamental equation, delving beyond the basic calculation to uncover its significance in various mathematical fields, its historical context, and its surprising applications in everyday life. Understanding 2 x 2 = 4 isn't just about rote memorization; it's about grasping the underlying principles of multiplication and its far-reaching consequences.
Understanding the Fundamentals: What is Multiplication?
Multiplication, at its core, is a form of repeated addition. When we say 2 x 2, we're essentially saying "two groups of two." This can be visualized in several ways:
- Using Objects: Imagine two baskets, each containing two apples. Counting all the apples gives us a total of four.
- Number Line: Start at zero on a number line. Jump two spaces twice (two jumps of two units). You land on four.
- Arrays: Arrange two rows of two objects each. Counting the objects reveals a total of four.
These visual representations are crucial, especially when introducing multiplication to young learners. They bridge the abstract concept of multiplication with concrete examples, fostering a deeper understanding.
The History of Multiplication: From Ancient Civilizations to Modern Mathematics
The concept of multiplication, though represented differently across cultures, has ancient roots. Evidence suggests that basic multiplicative principles were understood even in prehistoric times through counting objects and patterns. Early civilizations like the Babylonians and Egyptians developed sophisticated methods for multiplication, utilizing various techniques like doubling and halving. The development of the multiplication table, a cornerstone of arithmetic education, greatly streamlined the process, making calculations faster and more efficient. The evolution from these early methods to the concise notation we use today – the "x" symbol and the equals sign – demonstrates a remarkable progression in mathematical representation and understanding.
Beyond the Basics: Exploring the Properties of Multiplication
The seemingly simple equation, 2 x 2 = 4, embodies several crucial properties of multiplication:
- Commutative Property: This states that the order of numbers in a multiplication equation doesn't affect the result. 2 x 2 is the same as 2 x 2. This seemingly obvious fact is a fundamental principle used extensively in more complex mathematical operations.
- Associative Property: This property allows us to group numbers in different ways without changing the outcome. For instance, if we were multiplying 2 x 2 x 2, we could calculate (2 x 2) x 2 or 2 x (2 x 2) and still get 8. This is especially useful when dealing with multiple factors.
- Identity Property: Multiplying any number by 1 results in the same number. This might seem trivial, but it’s a fundamental property used in algebraic manipulations and other advanced mathematical concepts.
- Distributive Property: This property is critical when dealing with expressions involving addition and multiplication. It states that a x (b + c) = (a x b) + (a x c). This is used extensively in simplifying complex algebraic expressions and solving equations.
Applications of Multiplication: From Everyday Life to Advanced Mathematics
The simple act of calculating 2 x 2 = 4 has far-reaching consequences. Its applications extend across numerous fields:
- Everyday Calculations: From calculating the cost of two items at $2 each to determining the area of a square with 2-unit sides, multiplication is integral to our daily lives. We use it without even consciously thinking about it – it’s embedded in our routines.
- Geometry and Measurement: Calculating areas and volumes relies heavily on multiplication. From finding the area of a rectangle (length x width) to determining the volume of a cube (length x width x height), multiplication is fundamental to geometrical calculations.
- Algebra: Multiplication is a core operation in algebra, used to simplify expressions, solve equations, and manipulate variables. It forms the basis of polynomial operations and many other algebraic techniques.
- Calculus: Though more advanced, calculus uses multiplication in its core concepts, particularly in differentiation and integration. The process of finding derivatives and integrals often involves multiplication and its related operations.
- Computer Science: Binary arithmetic, the foundation of computer operations, heavily relies on multiplication. Bitwise operations, fundamental in programming, use multiplicative principles.
- Physics and Engineering: Calculations in physics and engineering often involve multiplication. From calculating forces and velocities to determining energy and power, multiplication is essential for solving complex problems.
- Finance: Calculating interest, profits, and losses all rely heavily on multiplication. It's an essential tool for any financial calculation, from simple budgeting to complex financial modeling.
2 x 2 = 4: A Stepping Stone to Higher Mathematics
While seemingly simple, 2 x 2 = 4 provides a fundamental understanding of numerical relationships. This basic equation serves as a stepping stone to more advanced mathematical concepts:
- Exponents: Understanding multiplication lays the groundwork for exponents. 2 x 2 can be represented as 2². This simple representation opens the door to understanding exponential growth and decay, crucial in various fields like population dynamics and finance.
- Matrices: In linear algebra, matrices involve arrays of numbers, and multiplication of matrices is a fundamental operation with numerous applications in various scientific fields.
- Abstract Algebra: The properties of multiplication explored earlier—commutativity, associativity, etc.—form the basis of abstract algebra, a branch of mathematics dealing with abstract structures and their properties. These principles are fundamental to group theory and ring theory.
Addressing Common Misconceptions
While 2 x 2 = 4 seems straightforward, some common misconceptions exist, particularly when introducing multiplication to younger learners:
- Confusion with Addition: Students sometimes confuse multiplication with addition. Understanding the difference between repeated addition and simple addition is crucial.
- Difficulty Visualizing Multiplication: Visual aids and real-world examples help students grasp the concept of multiplication.
- Memorization vs. Understanding: Rote memorization of multiplication tables, while useful, shouldn't replace a deep understanding of the underlying principles.
Frequently Asked Questions (FAQ)
Q: What is the inverse operation of multiplication?
A: The inverse operation of multiplication is division. Just as 2 x 2 = 4, 4 / 2 = 2.
Q: Is multiplication always commutative?
A: In standard arithmetic, yes, multiplication is always commutative. However, in certain advanced mathematical contexts (like matrix multiplication), this property might not always hold true.
Q: Why is understanding multiplication important?
A: Understanding multiplication is crucial because it's a fundamental building block for numerous mathematical concepts and applications in various fields. It's essential for everyday calculations, scientific pursuits, and technological advancements.
Q: How can I help children learn multiplication?
A: Use visual aids, real-world examples, games, and interactive activities to make learning multiplication fun and engaging. Focus on understanding the underlying principles rather than just rote memorization.
Conclusion: The Enduring Significance of 2 x 2 = 4
The equation 2 x 2 = 4, while seemingly simple, represents a profound mathematical concept with far-reaching implications. From its historical origins to its applications in advanced mathematics and various fields, this fundamental equation demonstrates the power and beauty of mathematical principles. Understanding its underlying concepts, properties, and implications is not just about mastering a basic calculation; it's about unlocking a deeper understanding of the mathematical world and its integral role in shaping our lives. The journey from grasping the simple act of counting two groups of two apples to comprehending the complexities of advanced mathematical concepts all begins with this seemingly simple equation. It's a testament to the elegance and power of mathematics, highlighting how a foundational concept can serve as a gateway to a world of endless possibilities.
Latest Posts
Latest Posts
-
50 Percent Off 40
Sep 23, 2025
-
What Animals Eat Zooplankton
Sep 23, 2025
-
12 Divided By 40
Sep 23, 2025
-
225 Divided By 3
Sep 23, 2025
-
2 Percent Of 8
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.