3 8 5 12
renascent
Sep 16, 2025 · 6 min read
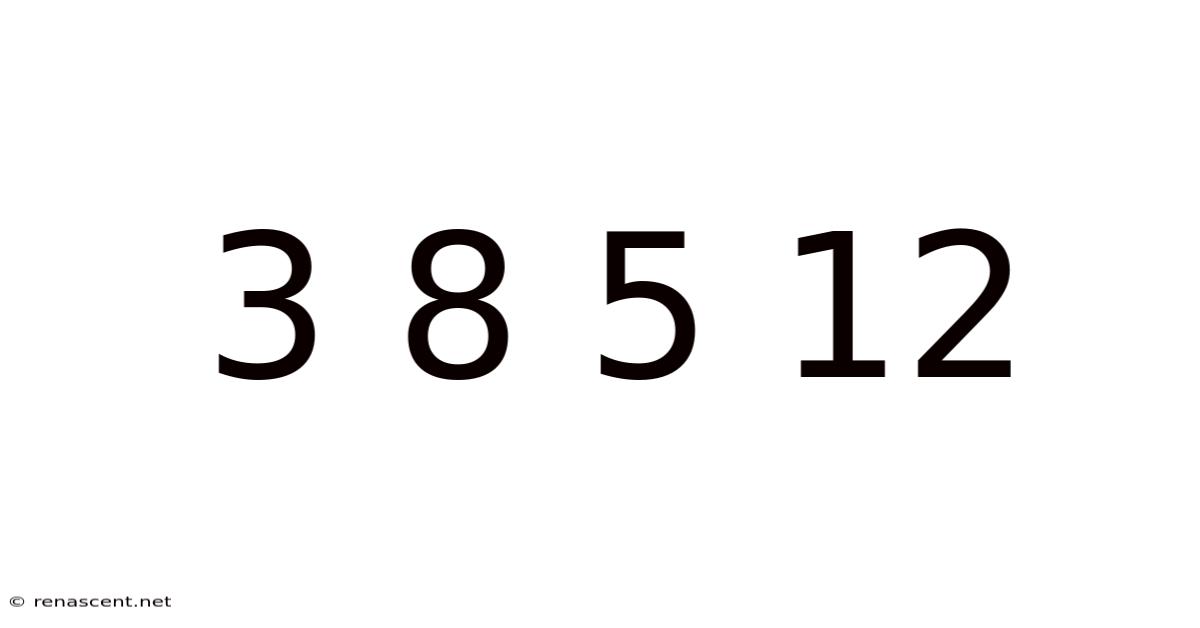
Table of Contents
Decoding the Sequence: Exploring the Mysteries of 3, 8, 5, 12
The seemingly simple sequence 3, 8, 5, 12 might appear innocuous at first glance. However, the beauty of mathematics lies in its ability to reveal hidden patterns and underlying structures within even the most basic-looking numerical sets. This article delves deep into the possible interpretations and mathematical explorations behind this sequence, exploring various approaches and uncovering the rich tapestry of possibilities. Understanding this sequence isn't just about finding a solution; it's about developing a mathematical mindset and appreciating the diversity of approaches to problem-solving. We'll explore different perspectives, from simple arithmetic progressions to more complex mathematical concepts, showcasing the power of logical reasoning and creative thinking.
Introduction: The Allure of Number Sequences
Number sequences have captivated mathematicians and puzzle enthusiasts for centuries. They serve as a fantastic training ground for developing critical thinking skills and exploring fundamental mathematical concepts. The sequence 3, 8, 5, 12 presents a fascinating challenge because it lacks an immediately obvious pattern. This ambiguity allows for multiple interpretations and encourages exploration of various mathematical tools and techniques. There isn't one single "correct" answer; instead, the journey of discovering possible patterns is the essence of the exercise.
Method 1: Analyzing Differences and Exploring Arithmetic Progressions
One common approach to analyzing number sequences is to examine the differences between consecutive terms. Let's apply this to our sequence:
- Difference between 8 and 3: 8 - 3 = 5
- Difference between 5 and 8: 5 - 8 = -3
- Difference between 12 and 5: 12 - 5 = 7
At first glance, the differences (5, -3, 7) don't reveal a clear arithmetic progression. However, we can explore other possibilities. Perhaps the differences themselves form a pattern, or maybe we need to consider other mathematical operations.
Method 2: Exploring Quadratic Relationships
Let's consider the possibility of a quadratic relationship. A quadratic sequence has second differences that are constant. Let's calculate the second differences:
- Difference between -3 and 5: -3 - 5 = -8
- Difference between 7 and -3: 7 - (-3) = 10
Again, we don't see a consistent pattern. This suggests that a simple quadratic relationship is unlikely.
Method 3: Investigating Recursive Relationships
A recursive relationship defines a term in the sequence based on previous terms. This approach often involves identifying a formula that relates each term to one or more preceding terms. For instance, we could explore if there is a relationship where the next term is a function of the previous terms. Let's explore some hypothetical recursive relationships:
- Hypothesis 1: Could the next term be the sum of the two preceding terms? This doesn't hold (3 + 8 ≠ 5, 8 + 5 ≠ 12).
- Hypothesis 2: Could the next term be a combination of addition and subtraction involving previous terms? This requires more extensive trial and error and might lead to a solution, but it's not guaranteed.
Method 4: Considering Modular Arithmetic and Cyclical Patterns
While the differences between consecutive terms didn't initially reveal a clear pattern, we could explore modular arithmetic. Modular arithmetic deals with remainders after division. Let's examine the remainders when each number is divided by a specific integer:
- Dividing by 2: remainders are 1, 0, 1, 0 (potential alternating pattern)
- Dividing by 3: remainders are 0, 2, 2, 0 (no obvious pattern)
- Dividing by 5: remainders are 3, 3, 0, 2 (no obvious pattern)
The remainders when divided by 2 suggest a potential alternating pattern, but this needs further investigation to confirm if it is part of a larger pattern.
Method 5: Looking for Prime Numbers and Factorizations
Let's analyze the prime factorization of each number:
- 3: 3
- 8: 2 x 2 x 2
- 5: 5
- 12: 2 x 2 x 3
There's no immediately obvious pattern in the prime factorizations. However, this doesn't rule out the possibility of a more subtle relationship involving prime factors or their combinations. Further analysis involving the number of prime factors or the types of prime factors might reveal a hidden pattern.
Method 6: Exploring Geometric Progressions and Ratios
While unlikely given the nature of the numbers, we can investigate the ratios between consecutive terms:
- 8/3 ≈ 2.67
- 5/8 = 0.625
- 12/5 = 2.4
The ratios are inconsistent, eliminating the possibility of a simple geometric progression.
Method 7: Introducing External Variables or Context
Sometimes, a sequence's meaning becomes clear only when additional context is provided. If this sequence were part of a larger problem, additional information might unlock the hidden pattern. For instance, the sequence could represent coordinates, measurements, or codes within a broader system. Without this context, it remains challenging to definitively determine the underlying principle.
Method 8: Advanced Mathematical Techniques
More advanced mathematical concepts could also be applied, such as generating functions, difference equations, or even exploring connections to other mathematical fields like graph theory or combinatorics. However, these methods are usually reserved for more complex sequences where simpler methods have failed.
Conclusion: The Open-Ended Nature of Mathematical Exploration
The sequence 3, 8, 5, 12 illustrates the fascinating and sometimes challenging nature of mathematical problem-solving. While we haven't found a definitive, universally accepted pattern, the exploration itself has been rewarding. We've applied various mathematical techniques, from simple arithmetic to more sophisticated approaches. The lack of an immediately obvious solution highlights the importance of persistence, creativity, and a willingness to explore multiple avenues. The true value lies not just in finding an answer but in the process of investigation and the development of critical thinking skills. It's a testament to the rich complexity and endless possibilities within the world of mathematics. Further exploration might involve using software to look for more complex patterns or exploring correlations with other numerical data sets. The sequence remains an open invitation for further mathematical inquiry.
Frequently Asked Questions (FAQ)
Q: Is there a single correct answer to this sequence problem?
A: No. The absence of an immediately apparent pattern allows for multiple interpretations and possible solutions. The process of exploring different methods and possibilities is the core value of this type of exercise.
Q: What mathematical skills are improved by solving such problems?
A: These exercises strengthen critical thinking, problem-solving skills, logical reasoning, and the ability to apply various mathematical concepts creatively.
Q: Are there similar problems I can try?
A: Yes. Many other number sequences with hidden patterns can be found online or in mathematics textbooks. Searching for "number sequence puzzles" or "mathematical patterns" will yield a plethora of challenging and rewarding exercises.
Q: What if I can't find a pattern?
A: That's perfectly fine. The absence of an obvious pattern doesn't mean you've failed. It simply indicates that the sequence might require more advanced techniques or additional context for a solution to be revealed. It's a valuable learning experience regardless of the outcome.
This exploration of the sequence 3, 8, 5, 12 highlights the multifaceted nature of mathematical problem-solving and the enduring appeal of numerical patterns. The journey of discovery, even without a conclusive answer, is a rewarding testament to the power of mathematical thinking.
Latest Posts
Latest Posts
-
Meaning Of Non Punitive
Sep 16, 2025
-
71 Inches Into Feet
Sep 16, 2025
-
Ch3 C O H
Sep 16, 2025
-
Poems With Personification Examples
Sep 16, 2025
-
3 Divided By 29
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3 8 5 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.