35 Divided By 7
renascent
Sep 18, 2025 · 6 min read
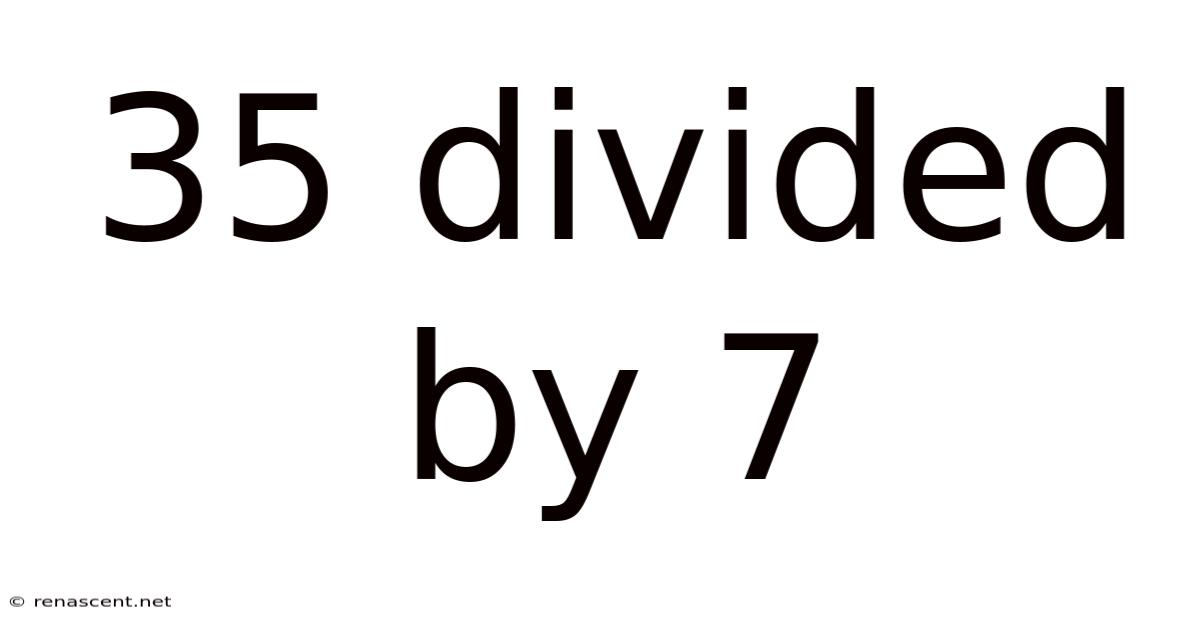
Table of Contents
35 Divided by 7: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 35 divided by 7, delving far beyond the immediate answer. We'll uncover the underlying principles of division, explore its various applications in everyday life and complex mathematical concepts, and even touch upon the historical context of this fundamental arithmetic operation. Understanding division, even at this basic level, forms the bedrock for more advanced mathematical understanding. This comprehensive guide will leave you with a solid grasp of not just the answer to 35 divided by 7, but also the broader implications of this mathematical process.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the case of 35 divided by 7 (often written as 35 ÷ 7, 35/7, or 7⟌35), we're asking: "How many times does 7 fit into 35?"
The answer, of course, is 5. This means that if you have 35 objects and you want to divide them equally among 7 groups, each group will receive 5 objects. This simple concept lays the foundation for understanding more complex division problems.
Different Ways to Visualize 35 Divided by 7
Visualizing the problem can make it easier to understand, especially for beginners. Here are a few ways to represent 35 divided by 7:
-
Using Objects: Imagine having 35 marbles. If you distribute them evenly into 7 bags, how many marbles will be in each bag? Counting them out will show you there are 5 marbles per bag.
-
Using a Number Line: Start at 0 on a number line. Jump 7 units at a time. How many jumps do you need to reach 35? You'll need 5 jumps, again illustrating that 35 divided by 7 is 5.
-
Using Arrays: You can arrange 35 objects into a rectangular array with 7 columns. The number of rows will represent the answer. You’ll find you need 5 rows, confirming the answer.
The Relationship Between Division and Multiplication
Division and multiplication are inverse operations. This means that they "undo" each other. If 7 multiplied by 5 equals 35 (7 x 5 = 35), then 35 divided by 7 equals 5 (35 ÷ 7 = 5), and 35 divided by 5 equals 7 (35 ÷ 5 = 7). This reciprocal relationship is crucial for solving many mathematical problems.
Division with Remainders: Stepping Beyond Whole Numbers
While 35 divided by 7 results in a whole number (5), not all division problems are so neat. Consider dividing 37 by 7. 7 goes into 37 five times (7 x 5 = 35), but there are 2 left over. This "leftover" is called the remainder. We can express this as 37 ÷ 7 = 5 with a remainder of 2, or sometimes written as 5 R2. Understanding remainders is essential for working with larger numbers and more complex divisions.
Applications of Division in Everyday Life
Division isn't just a classroom exercise; it's a fundamental skill used daily. Here are some examples:
-
Sharing: Dividing snacks, toys, or chores equally among friends or family members.
-
Cooking: Following recipes that require dividing ingredients into portions.
-
Shopping: Calculating the unit price of an item to determine the best buy.
-
Travel: Determining the average speed or fuel consumption during a journey.
-
Finance: Dividing expenses among roommates or calculating the monthly payment on a loan.
Division in Advanced Mathematics
Beyond everyday applications, division plays a vital role in various advanced mathematical concepts:
-
Fractions: A fraction (like 35/7) represents a division problem. The numerator (35) is divided by the denominator (7).
-
Algebra: Solving algebraic equations often involves division to isolate variables.
-
Calculus: Division is fundamental to many calculus concepts, including derivatives and integrals.
-
Statistics: Calculating averages (means) and other statistical measures often requires division.
-
Number Theory: Division plays a central role in number theory, including concepts like prime numbers and divisibility rules.
The History of Division
The concept of division has ancient roots. Evidence suggests that early civilizations used various methods for dividing quantities. While the modern symbols and algorithms we use today developed over centuries, the fundamental concept of dividing quantities into equal parts has been a cornerstone of mathematics for millennia. Ancient Egyptian mathematicians, for instance, developed sophisticated methods for handling division problems, laying groundwork for future mathematical advancements.
Common Mistakes to Avoid When Dividing
Even seemingly simple division problems can trip people up. Here are some common mistakes to watch out for:
-
Incorrect Order of Operations: Remember the order of operations (PEMDAS/BODMAS). Division should be performed before addition or subtraction unless parentheses dictate otherwise.
-
Misunderstanding Remainders: Make sure you understand how to interpret and represent remainders correctly.
-
Errors in Calculation: Double-check your calculations to minimize errors. Using a calculator can help, but understanding the underlying process is crucial.
-
Confusing Dividend and Divisor: Remember that the dividend is the number being divided (35 in our example), and the divisor is the number you're dividing by (7).
Frequently Asked Questions (FAQ)
Q: What is the quotient in 35 divided by 7?
A: The quotient is the result of the division, which is 5.
Q: Can I use a calculator to solve 35 divided by 7?
A: Yes, absolutely! Calculators are helpful tools for solving division problems, especially with larger numbers. However, understanding the underlying principles of division is still crucial.
Q: What if I have a decimal number as the dividend or divisor?
A: Dividing with decimals involves similar principles but requires additional steps. You'll often need to adjust decimal places to perform the division accurately.
Q: How can I improve my division skills?
A: Practice is key! Start with simple problems and gradually work your way up to more complex ones. Use different methods (visual aids, calculators) to reinforce your understanding.
Conclusion: Beyond the Answer
While the answer to 35 divided by 7 is simply 5, this article aimed to show you that this seemingly basic calculation is far more significant than it initially appears. Understanding division is not just about finding answers; it's about grasping a fundamental mathematical concept with far-reaching implications, impacting various aspects of our daily lives and advanced mathematical explorations. From simple everyday tasks to complex scientific calculations, division serves as an essential building block in the world of numbers. Mastering this fundamental skill unlocks a deeper appreciation of mathematics and its practical applications in countless situations. So next time you encounter a division problem, remember the depth and breadth of this seemingly simple operation.
Latest Posts
Latest Posts
-
Estate In Fee Simple
Sep 18, 2025
-
Expanded Notation In Maths
Sep 18, 2025
-
Michael C Hall Younger
Sep 18, 2025
-
70 Mph In Km
Sep 18, 2025
-
Acrylic Powder And Liquid
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 35 Divided By 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.