36/40 As A Percentage
renascent
Sep 20, 2025 · 5 min read
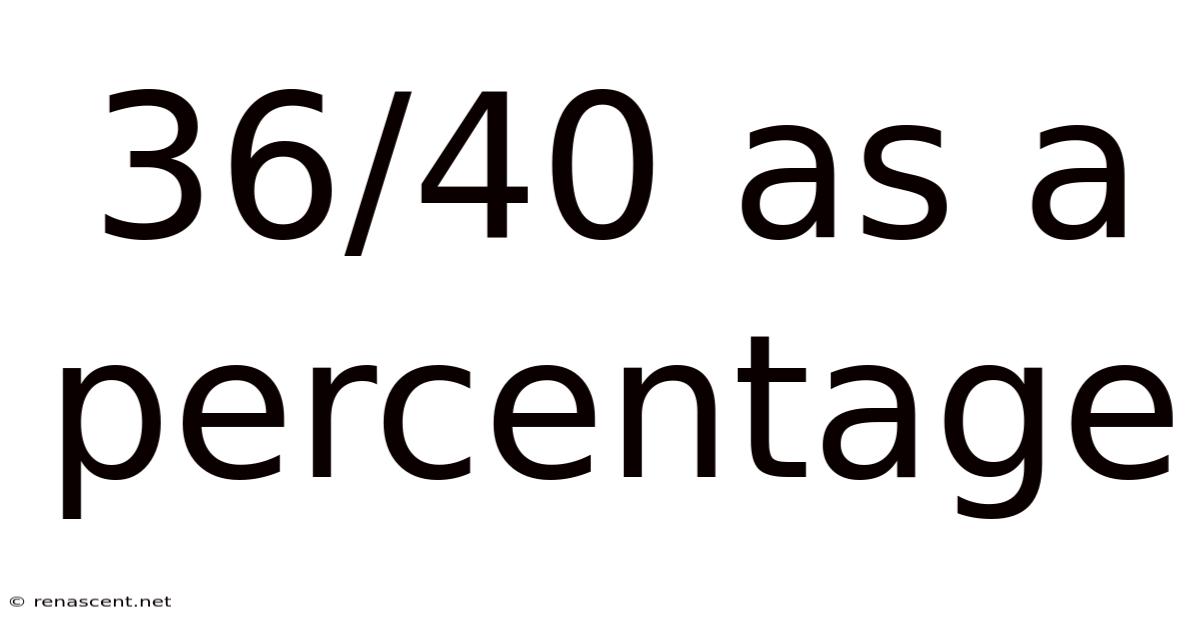
Table of Contents
Understanding 36/40 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications across numerous fields, from calculating grades to understanding financial data. This comprehensive guide will delve into the process of converting 36/40 into a percentage, exploring the underlying principles and providing practical examples. We'll also address common questions and misconceptions surrounding percentage calculations. Understanding this seemingly simple conversion lays a solid foundation for more complex percentage-based problems.
Understanding Fractions and Percentages
Before diving into the conversion of 36/40, let's establish a clear understanding of fractions and percentages. A fraction represents a part of a whole. The numerator (top number) indicates the portion considered, while the denominator (bottom number) represents the total. For instance, 36/40 signifies 36 parts out of a total of 40 parts.
A percentage, denoted by the symbol %, represents a fraction where the denominator is always 100. It indicates how many parts of a whole there are per 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 36/40 to a Percentage: Step-by-Step Guide
There are two primary methods to convert the fraction 36/40 to a percentage:
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This method involves two steps:
-
Convert the fraction to a decimal: To do this, divide the numerator (36) by the denominator (40).
36 ÷ 40 = 0.9
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%).
0.9 × 100 = 90%
Therefore, 36/40 is equal to 90%.
Method 2: Directly Converting the Fraction to a Percentage
This method involves a single step:
-
Set up a proportion: We want to find the equivalent percentage, which means finding a fraction with a denominator of 100 that is equal to 36/40. We can set up a proportion:
36/40 = x/100
-
Solve for x: To solve for x, cross-multiply:
40x = 3600
-
Divide: Divide both sides by 40:
x = 3600 ÷ 40 = 90
Therefore, x = 90, meaning 36/40 is equal to 90%.
Simplifying Fractions Before Conversion
While both methods are equally valid, simplifying the fraction before conversion can often make the calculation easier. In this case, 36 and 40 share a common factor of 4. Simplifying the fraction:
36 ÷ 4 = 9 40 ÷ 4 = 10
This simplifies 36/40 to 9/10. Now, converting 9/10 to a percentage is straightforward:
9 ÷ 10 = 0.9 0.9 × 100 = 90%
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in various real-world scenarios:
- Academic Grades: If a student answers 36 out of 40 questions correctly on a test, their score is 90%.
- Financial Calculations: Percentage changes in stock prices, interest rates, and discounts are all calculated using this principle.
- Data Analysis: Representing data in percentages provides a clear and concise way to visualize proportions and trends.
- Sales and Marketing: Calculating profit margins, sales growth, and customer conversion rates often involves percentage calculations.
Addressing Common Misconceptions
Some common misconceptions surrounding percentage calculations include:
- Confusing percentages with decimals: Remember to multiply the decimal by 100 to convert it to a percentage.
- Incorrectly interpreting percentages: A percentage always represents a proportion of a whole, not an absolute value. For example, 90% of 100 is different from 90% of 500.
- Difficulty with complex fractions: Simplifying fractions before conversion can greatly simplify the process.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a fraction, decimal, and percentage?
A: A fraction represents a part of a whole using a numerator and denominator. A decimal represents a fraction using base-10 notation. A percentage represents a fraction where the denominator is 100.
Q2: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have a division function that can be used to convert fractions to decimals, followed by multiplication by 100 to convert to percentages.
Q3: What if the fraction doesn't simplify easily?
A: Even if the fraction doesn't simplify easily, you can still use the division method (Method 1) to accurately convert it to a percentage.
Q4: How do I calculate a percentage of a number?
A: To calculate a percentage of a number, convert the percentage to a decimal (divide by 100) and then multiply by the number. For example, 90% of 200 is 0.9 x 200 = 180.
Q5: What are some real-world examples beyond grades and finance?
A: Percentages are used extensively in fields like science (e.g., calculating concentrations of solutions), engineering (e.g., calculating efficiency of machines), and weather forecasting (e.g., expressing the probability of precipitation).
Conclusion
Converting 36/40 to a percentage, resulting in 90%, is a straightforward process with practical applications across numerous fields. Understanding the underlying principles of fractions and percentages, and mastering the conversion methods described above, will equip you with essential mathematical skills applicable to various real-world situations. Remember to practice regularly and explore different examples to build your confidence and proficiency in percentage calculations. By understanding these fundamental concepts, you'll be better equipped to tackle more complex percentage-related problems and confidently interpret data presented in percentage form. The ability to seamlessly convert fractions to percentages is a key skill for success in many academic and professional settings.
Latest Posts
Latest Posts
-
Fahrenheit 90 To Celsius
Sep 20, 2025
-
Music For Contemporary Dance
Sep 20, 2025
-
1 2 X 2 1 4
Sep 20, 2025
-
Lewis Structure Of Ethene
Sep 20, 2025
-
How I See Myself
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 36/40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.