4 Divided By 360
renascent
Sep 24, 2025 · 6 min read
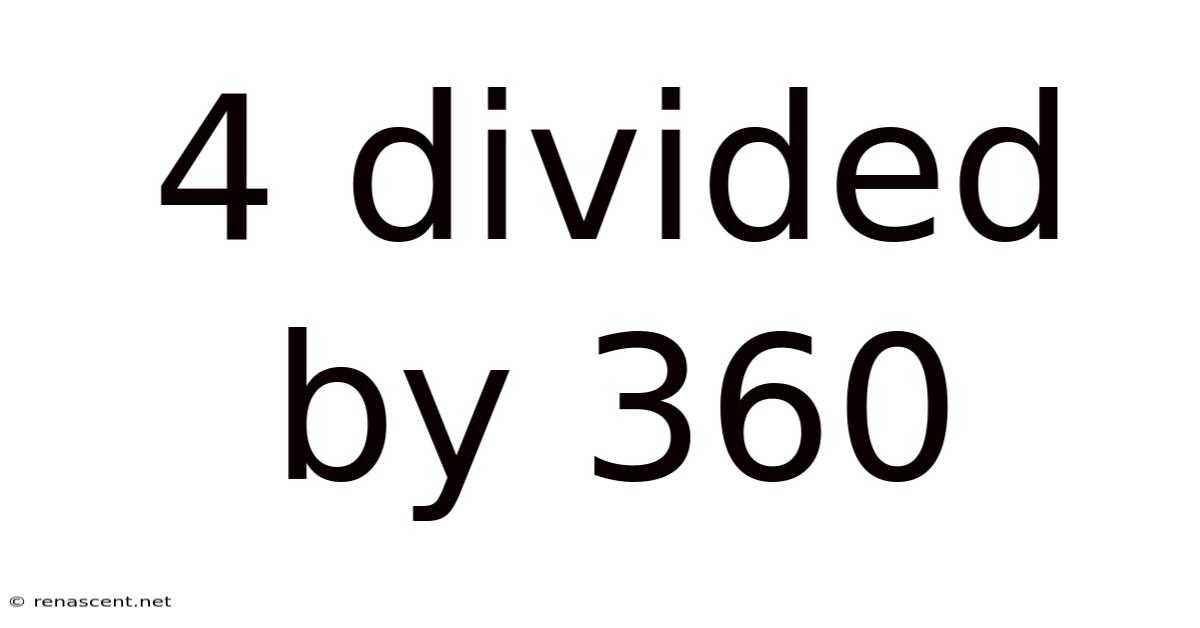
Table of Contents
Unveiling the Mystery: 4 Divided by 360 – A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 4 divided by 360, delving far beyond the immediate answer to uncover the underlying mathematical principles and practical applications. We'll examine the process of division, explore different methods of solving this problem, and discuss the significance of this type of calculation in various fields, from basic arithmetic to advanced mathematics and real-world scenarios. Understanding this seemingly basic calculation opens doors to a broader comprehension of fractional arithmetic and its relevance in our daily lives. We'll also address common misconceptions and frequently asked questions to ensure a comprehensive understanding for readers of all levels.
Understanding the Basics: Division and its Fundamentals
Before diving into 4 divided by 360, let's refresh our understanding of division. Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the expression "a ÷ b," 'a' is the dividend (the number being divided), and 'b' is the divisor (the number dividing the dividend). The result is called the quotient.
In our case, 4 is the dividend and 360 is the divisor. We are essentially asking: "If we divide 4 into 360 equal parts, how large is each part?"
Calculating 4 Divided by 360: Methods and Solutions
The most straightforward way to calculate 4 ÷ 360 is using a calculator or performing long division. However, let's explore the process in detail:
1. Long Division:
While using a calculator is efficient, understanding the long division method provides a deeper grasp of the calculation. The process is as follows:
- Since 4 is smaller than 360, the quotient will be less than 1. We can express the result as a fraction: 4/360.
- We can simplify this fraction by finding the greatest common divisor (GCD) of 4 and 360. The GCD of 4 and 360 is 4.
- Dividing both the numerator and denominator by 4, we get: (4 ÷ 4) / (360 ÷ 4) = 1/90.
Therefore, 4 divided by 360 is equal to 1/90.
2. Decimal Representation:
The fraction 1/90 can be converted to a decimal by performing the division: 1 ÷ 90 ≈ 0.011111...
This decimal representation is a recurring decimal, meaning the digit 1 repeats infinitely. For practical purposes, we may round this to a certain number of decimal places, depending on the required level of accuracy.
3. Percentage Representation:
We can also express the result as a percentage: (1/90) * 100% ≈ 1.11%. This indicates that 4 represents approximately 1.11% of 360.
Beyond the Calculation: Understanding the Significance of Fractions and Decimals
The result of 4 divided by 360, whether expressed as a fraction (1/90) or a decimal (approximately 0.0111), highlights the importance of understanding fractions and decimals in mathematics. These represent parts of a whole and are essential for various applications:
-
Measurement and Proportion: Fractions and decimals are fundamental in measuring quantities, comparing proportions, and scaling objects. Imagine calculating the proportion of a specific ingredient in a recipe or determining the scale of a model compared to its real-world counterpart. The calculation of 4/360 might represent a small portion of a larger quantity in such scenarios.
-
Geometry and Trigonometry: In geometry and trigonometry, ratios and proportions are frequently used. For example, calculating angles in a circle using radians involves fractions and decimals.
-
Financial Calculations: Percentages, which are directly related to fractions and decimals, are crucial in finance for calculating interest rates, discounts, and taxes. Understanding the meaning of 1.11% derived from our calculation helps in interpreting these financial contexts.
-
Data Analysis and Statistics: Fractions and decimals are ubiquitous in data analysis and statistics. They are used to represent probabilities, proportions within datasets, and various statistical measures.
-
Computer Science and Programming: Fractions and decimals are used in various aspects of computer science and programming, including representing floating-point numbers, image processing and computational graphics.
Real-World Applications: Examples of 4/360 in Practice
Although seemingly a simple calculation, the concept behind 4 divided by 360 can be applied to various real-world situations:
-
Circular Motion: Imagine a circular object rotating. If the object completes 4 degrees of rotation out of a full 360-degree rotation, the fraction 4/360 represents the proportion of the circle's rotation completed. This could be useful in calculating angular speed or in mechanical engineering.
-
Surveys and Sampling: If a survey is conducted with 360 participants, and only 4 responded in a particular way, the fraction 4/360 would indicate the proportion of respondents holding that specific opinion.
-
Resource Allocation: Imagine allocating a budget of 360 units. If 4 units are allocated to a specific project, 4/360 represents the fraction of the budget allocated to that project. This concept is frequently used in business and project management.
-
Scientific Measurements: In various scientific experiments, measuring very small proportions is common. The concept of 4/360 can be scaled to represent minuscule quantities or proportions in experimental results.
Addressing Common Questions and Misconceptions
Q: Why is it important to simplify the fraction 4/360 to 1/90?
A: Simplifying fractions makes them easier to understand and compare. 1/90 gives a clearer representation of the proportion than 4/360. It also helps in further calculations, as smaller numbers are easier to work with.
Q: What if I get a slightly different decimal value when using a calculator?
A: Calculators may round off the decimal representation of 1/90. The exact decimal value is a non-terminating repeating decimal (0.01111...). The difference is due to rounding and depends on the calculator's precision.
Q: Are there other ways to represent the result besides a fraction and decimal?
A: Yes. You can represent the result as a percentage (approximately 1.11%), a ratio (1:90), or even using scientific notation (1.111 x 10⁻²). The best representation depends on the context and the desired level of precision.
Conclusion: The Power of a Simple Calculation
While seemingly basic, the calculation of 4 divided by 360 provides a powerful entry point into understanding fractions, decimals, and their wide-ranging applications in various fields. Mastering this simple division, and grasping the underlying principles, helps build a stronger foundation in mathematics and enhances problem-solving skills applicable to a multitude of real-world scenarios. Remember, even the smallest mathematical concepts can hold vast significance when we explore their deeper implications and practical uses. The seemingly insignificant 1/90 reveals the beauty and utility of fundamental mathematical principles.
Latest Posts
Latest Posts
-
100 Ounces To Ml
Sep 24, 2025
-
225 Mph To Kmh
Sep 24, 2025
-
45 Divided By 2
Sep 24, 2025
-
33 1 3 In Fraction
Sep 24, 2025
-
39 Degrees In Fahrenheit
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 360 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.