Square Root Of 112
renascent
Sep 18, 2025 · 6 min read
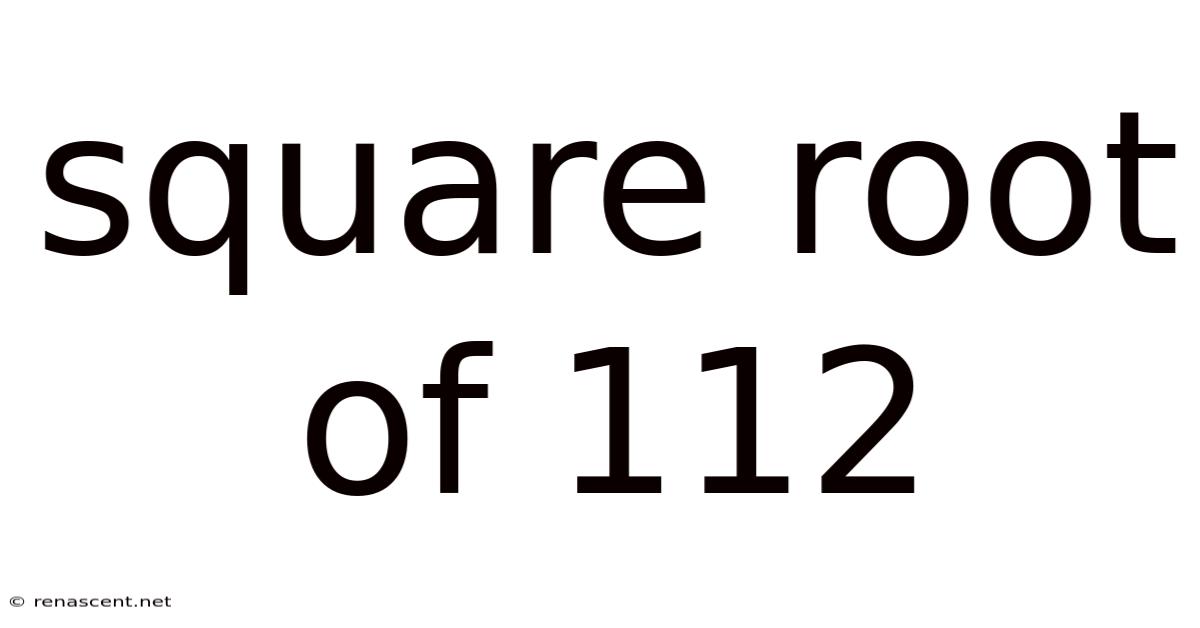
Table of Contents
Unveiling the Mysteries of the Square Root of 112: A Deep Dive into Calculation and Application
Finding the square root of a number might seem like a simple mathematical operation, but delving into the specifics, particularly for a number like 112, reveals a fascinating journey into the world of numbers and their properties. This article will explore the square root of 112, examining various methods of calculation, discussing its properties, and highlighting its applications in different fields. Understanding the square root of 112 is not just about getting a numerical answer; it's about grasping fundamental mathematical concepts and their real-world implications.
Introduction: What is a Square Root?
Before we embark on our exploration of the square root of 112, let's establish a clear understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because 3 multiplied by 3 equals 9. This is represented mathematically as √9 = 3. The square root symbol (√) indicates the operation of finding the principal square root, which is always the non-negative value.
The square root of 112, however, is not a whole number. This means it's an irrational number, a number that cannot be expressed as a simple fraction. Its value lies between 10 and 11, as 10² = 100 and 11² = 121. But how exactly do we calculate its value? Let's explore various methods.
Methods for Calculating the Square Root of 112
Several methods exist for calculating the square root of 112, ranging from simple estimation to sophisticated algorithms. Let's examine a few:
1. Estimation and Approximation:
The simplest approach is estimation. Since 112 lies between 100 (10²) and 121 (11²), we know the square root of 112 is between 10 and 11. We can refine this estimation by considering the proximity of 112 to 100 and 121. Being closer to 100, we can guess a value slightly above 10, perhaps around 10.5 or 10.6. This method provides a rough approximation, useful for quick estimations but not for precise calculations.
2. Prime Factorization:
Prime factorization is a powerful technique to simplify calculations involving square roots. We can break down 112 into its prime factors:
112 = 2 x 56 = 2 x 2 x 28 = 2 x 2 x 2 x 14 = 2 x 2 x 2 x 2 x 7 = 2⁴ x 7
Therefore, √112 = √(2⁴ x 7) = √2⁴ x √7 = 2²√7 = 4√7
This simplifies the square root to 4 times the square root of 7. While this doesn't provide a decimal value, it's a more precise representation than a simple estimation. We can then use a calculator or approximation methods to find the square root of 7 (approximately 2.646) and multiply by 4 to get a more accurate result.
3. The Babylonian Method (or Heron's Method):
This iterative method provides increasingly accurate approximations with each step. It starts with an initial guess (let's use 10.5) and refines it using the formula:
x_(n+1) = 0.5 * (x_n + (112/x_n))
Where:
- x_n is the current approximation
- x_(n+1) is the next, improved approximation
Let's perform a few iterations:
- Iteration 1: x_1 = 0.5 * (10.5 + (112/10.5)) ≈ 10.58
- Iteration 2: x_2 = 0.5 * (10.58 + (112/10.58)) ≈ 10.583
- Iteration 3: x_3 = 0.5 * (10.583 + (112/10.583)) ≈ 10.583
As you can see, the value converges quickly to approximately 10.583. This method offers a higher degree of accuracy compared to simple estimation.
4. Using a Calculator:
The most straightforward method for obtaining a precise decimal approximation of √112 is to use a calculator. Most calculators have a square root function that will directly provide the result, which is approximately 10.583.
Understanding the Irrational Nature of √112
As mentioned earlier, √112 is an irrational number. This means its decimal representation is non-terminating and non-repeating. It cannot be expressed as a simple fraction (a ratio of two integers). This irrationality arises from the fact that 112 is not a perfect square (a number that is the square of an integer). The presence of the prime factor 7, which does not have a whole number square root, contributes to this irrationality.
Applications of Square Roots
Understanding and calculating square roots is crucial across numerous fields:
-
Geometry: Calculating distances, areas, and volumes frequently involve square roots. For instance, finding the diagonal of a square or the hypotenuse of a right-angled triangle relies on the Pythagorean theorem, which utilizes square roots.
-
Physics: Many physical phenomena are described by equations involving square roots. For example, calculations related to velocity, acceleration, and energy often require calculating square roots.
-
Engineering: Structural engineers use square roots in calculations related to stress, strain, and stability. Civil engineers use them in surveying and road design.
-
Finance: Calculating compound interest and present value of investments involves square roots. Understanding standard deviation and variance in financial data analysis also relies on square root calculations.
-
Computer Graphics: Square roots are fundamental in computer graphics for calculating distances and transformations in 2D and 3D space. Rendering and animation processes rely heavily on these calculations.
-
Statistics: Calculating standard deviation, a critical measure of data dispersion, involves the square root of the variance.
Frequently Asked Questions (FAQ)
Q: Is there a simple way to memorize the square root of 112?
A: No, there isn't a simple way to memorize the exact value of √112 because it's an irrational number with a non-repeating decimal expansion. However, remembering that it's slightly above 10 (because 10² = 100 and 11² = 121) provides a useful approximation.
Q: Can I use a different initial guess in the Babylonian method?
A: Yes, the Babylonian method will still converge to the correct answer even with a different initial guess. However, a closer initial guess will generally lead to faster convergence.
Q: Why is prime factorization helpful in simplifying square roots?
A: Prime factorization allows us to identify perfect square factors within the number. By extracting these perfect square factors, we can simplify the square root expression, making calculations easier and providing a more manageable form.
Q: What are some common mistakes to avoid when calculating square roots?
A: Common mistakes include: * Incorrect application of the order of operations (PEMDAS/BODMAS) * Forgetting that the square root of a negative number is an imaginary number (involving i, where i² = -1). * Rounding errors during calculations, particularly in iterative methods.
Conclusion: The Significance of Understanding √112
The seemingly simple task of finding the square root of 112 reveals a depth of mathematical concepts and their widespread applications. From estimations and prime factorization to iterative methods and calculator usage, we've explored various techniques for calculating this value. Understanding the irrational nature of √112 and its practical applications underscores the importance of mastering fundamental mathematical principles. This knowledge isn’t just for academic purposes; it’s a vital tool for anyone working in fields that involve numbers and calculations, demonstrating the interconnectedness of mathematics with the real world. The journey to understand √112 has been more than just finding a number; it’s been a journey into the heart of mathematics itself.
Latest Posts
Latest Posts
-
X 3 2x 2
Sep 18, 2025
-
4 5 Cm To Inches
Sep 18, 2025
-
King Queen Crown Tattoo
Sep 18, 2025
-
The Innermost Electron Shell
Sep 18, 2025
-
2 X 2 10
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 112 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.