What Is 30 100
renascent
Sep 18, 2025 · 5 min read
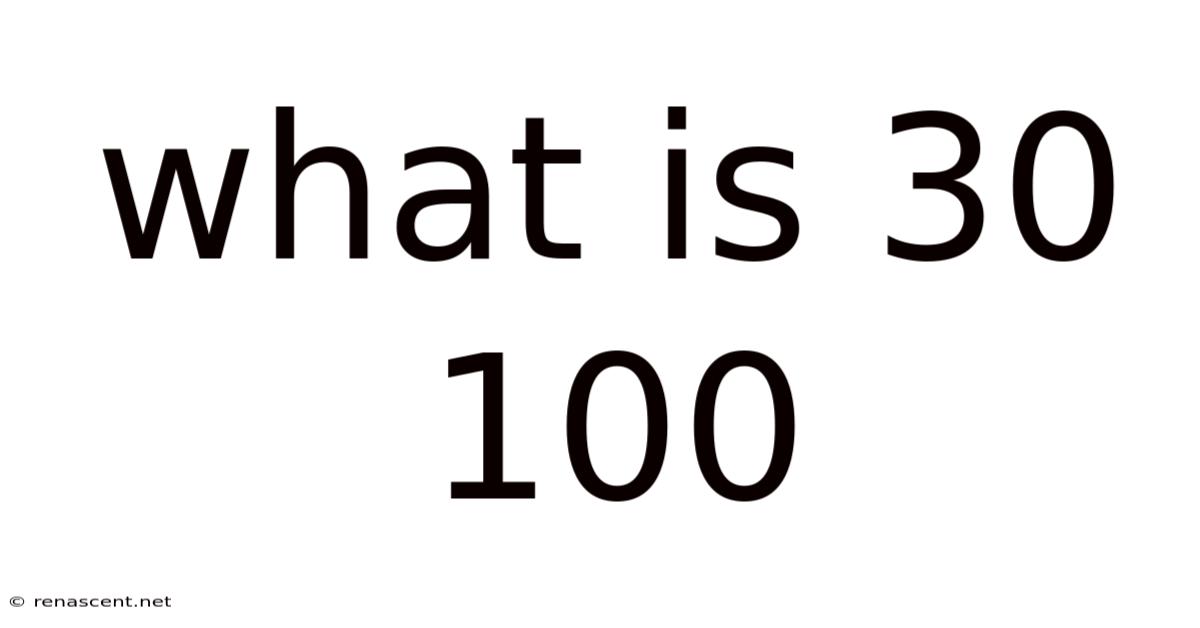
Table of Contents
Decoding 30/100: Understanding Percentage, Ratio, and Proportion
What does 30/100 mean? At first glance, it seems simple: a fraction. But understanding 30/100 unlocks a deeper understanding of crucial mathematical concepts like percentages, ratios, and proportions, applicable in various real-world scenarios from calculating discounts to understanding statistical data. This comprehensive guide will explore the multifaceted meaning of 30/100, providing clear explanations, practical examples, and addressing frequently asked questions.
Understanding the Basics: Fractions, Decimals, and Percentages
Before diving into the specifics of 30/100, let's establish a solid foundation. A fraction represents a part of a whole. In the fraction 30/100, 30 is the numerator (the part) and 100 is the denominator (the whole). This fraction can also be expressed as a decimal by dividing the numerator by the denominator: 30 ÷ 100 = 0.3.
A percentage is simply a fraction expressed as a portion of 100. Since our fraction has a denominator of 100, converting it to a percentage is straightforward: 30/100 is equal to 30%. This means 30 out of every 100 units represent 30%.
30/100 in Different Contexts: Real-World Applications
The interpretation of 30/100 varies depending on the context. Let's explore some practical examples:
-
Test Scores: If a student achieves 30/100 on a test, it means they answered 30 questions correctly out of a total of 100 questions. This translates to a score of 30%.
-
Sales and Discounts: A 30% discount on a product priced at $100 means a reduction of $30 (30/100 * $100 = $30), resulting in a final price of $70.
-
Surveys and Statistics: In a survey of 100 people, if 30 respond positively to a particular question, the positive response rate is 30%. This data can be crucial in market research, opinion polls, and other forms of data analysis.
-
Probability: In a scenario with 100 equally likely outcomes, if 30 outcomes favor a specific event, the probability of that event occurring is 30%.
Exploring Ratios and Proportions
30/100 can also be viewed as a ratio, expressing the relationship between two quantities. The ratio 30:100 simplifies to 3:10, indicating a proportion of 3 parts to every 10 parts. This concept is vital in various fields, such as:
-
Recipe Scaling: If a recipe calls for a 3:10 ratio of sugar to flour, you can scale it proportionally. For instance, if you use 30 grams of sugar, you'll need 100 grams of flour.
-
Map Scales: Maps frequently use ratios to represent distances. A scale of 1:100,000 means 1 unit on the map equals 100,000 units in reality. While not directly 30/100, understanding this foundational ratio concept is key to interpreting any ratio.
-
Mixing Solutions: In chemistry or other scientific fields, precise ratios are essential when mixing solutions. A 3:10 ratio might represent the proportion of solute to solvent.
Proportions are essentially statements of equality between two ratios. For example, the proportion 30/100 = x/200 can be solved to find the value of x (x = 60). This skill is indispensable for solving various practical problems involving scaling, percentages, and similar concepts. Understanding the proportion allows us to extrapolate from a known ratio to an unknown one. This is a powerful tool that extends beyond simple calculations.
Simplifying Fractions: A Deeper Dive into 30/100
The fraction 30/100 can be simplified by finding the greatest common divisor (GCD) of both the numerator and the denominator. The GCD of 30 and 100 is 10. Dividing both the numerator and denominator by 10, we simplify 30/100 to 3/10. This simplified fraction represents the same value but in a more concise form. This simplification is often beneficial for easier calculations and a clearer understanding of the proportion.
The ability to simplify fractions is a fundamental skill in mathematics. It's not merely about aesthetics; it's about efficiency and clarity. Simplifying allows for easier comparisons, quicker calculations, and a more intuitive grasp of the underlying relationships between numbers.
Beyond the Basics: Extending the Concept
While 30/100 might seem like a simple fraction, its implications extend beyond basic arithmetic. Understanding this concept lays the groundwork for more advanced mathematical concepts, including:
-
Algebra: Solving equations often involves working with fractions and percentages, building upon the foundational understanding developed by working with simple fractions like 30/100.
-
Statistics and Probability: Calculating probabilities, analyzing datasets, and understanding statistical significance frequently involves working with proportions and percentages, making an understanding of 30/100 essential for these areas.
-
Financial Literacy: Understanding percentages is crucial for managing personal finances, calculating interest rates, analyzing investment returns, and understanding various financial concepts.
Frequently Asked Questions (FAQ)
Q: How do I convert 30/100 to a percentage?
A: Since a percentage is a fraction out of 100, 30/100 is directly equivalent to 30%.
Q: What is the simplest form of 30/100?
A: The simplest form is 3/10. This is obtained by dividing both the numerator and denominator by their greatest common divisor, which is 10.
Q: How do I calculate 30% of a number?
A: To calculate 30% of a number, multiply the number by 0.3 (or 3/10). For example, 30% of 200 is 200 * 0.3 = 60.
Q: What is the difference between a ratio and a proportion?
A: A ratio compares two quantities, while a proportion states that two ratios are equal. 30:100 is a ratio; 30/100 = 60/200 is a proportion.
Q: Why is understanding 30/100 important?
A: Understanding 30/100 is crucial for developing a strong foundation in mathematics. It helps in understanding percentages, ratios, proportions, and other essential concepts applicable in diverse fields, including everyday life, academics, and professional settings.
Conclusion: Mastering the Fundamentals
While seemingly straightforward, understanding 30/100 unlocks a world of mathematical possibilities. From everyday calculations to complex statistical analysis, the ability to confidently work with fractions, decimals, percentages, ratios, and proportions is an invaluable skill. By mastering these fundamental concepts, you build a strong foundation for future mathematical explorations and real-world problem-solving. This comprehensive guide has explored the multifaceted nature of 30/100, illustrating its various interpretations and applications. Remember, the journey to mathematical proficiency begins with a solid grasp of the basics, and 30/100 provides an excellent starting point for that journey.
Latest Posts
Latest Posts
-
50 Percent Of 40
Sep 18, 2025
-
200 Micrograms To Mg
Sep 18, 2025
-
Wheels In Motion Ca
Sep 18, 2025
-
86 7 Kg To Stone
Sep 18, 2025
-
Methyl Red Ph Range
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.