X 3 Y 3
renascent
Sep 18, 2025 · 6 min read
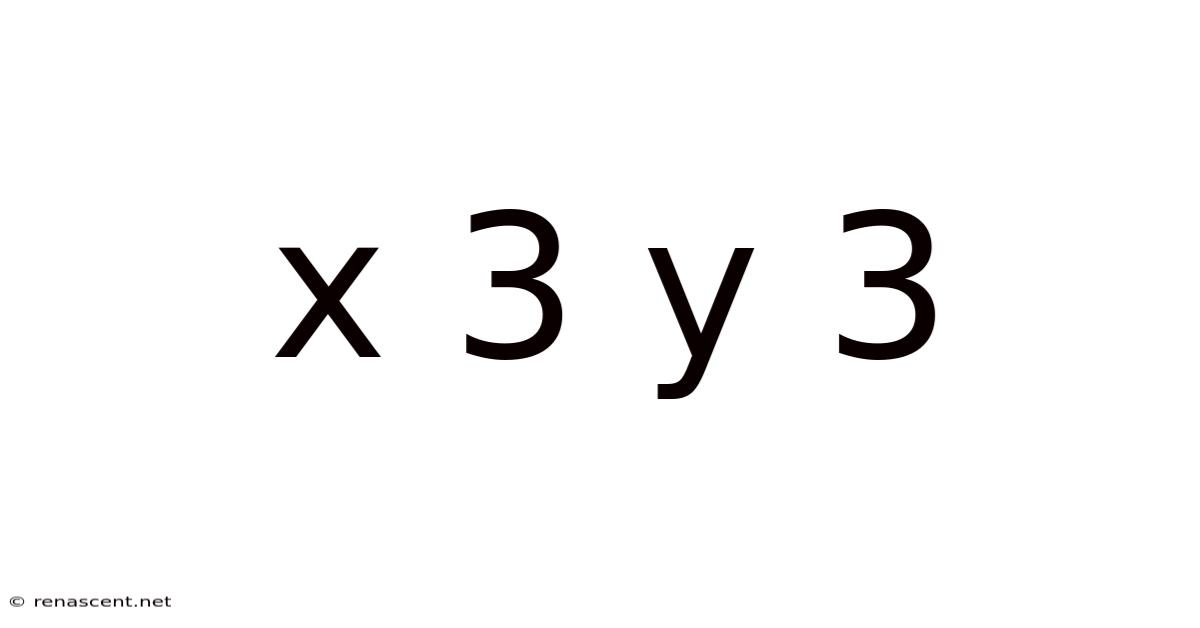
Table of Contents
Unraveling the Mysteries of x³ + y³: A Deep Dive into Sum of Cubes
The expression x³ + y³ might seem simple at first glance, a mere algebraic sum of two cubed variables. However, beneath its unassuming exterior lies a rich tapestry of mathematical concepts, applications, and elegant factorization techniques. This comprehensive guide will explore the intricacies of x³ + y³ — from its basic factorization to its surprising applications in various fields of mathematics and beyond. We'll cover its derivation, explore its geometric interpretations, and delve into practical examples to solidify your understanding. This will equip you with a thorough understanding of this seemingly simple yet profoundly significant algebraic expression.
Understanding the Factorization of x³ + y³
The cornerstone of understanding x³ + y³ lies in its factorization. Unlike the difference of cubes (x³ - y³), which factors neatly into (x - y)(x² + xy + y²), the sum of cubes requires a slightly different approach. The factorization of x³ + y³ is given by:
x³ + y³ = (x + y)(x² - xy + y²)
This seemingly simple equation opens doors to a wealth of mathematical possibilities. Let's break down why this factorization holds true.
Proof through Polynomial Long Division
One way to verify this factorization is through polynomial long division. If (x + y) is a factor of x³ + y³, then dividing x³ + y³ by (x + y) should yield a remainder of zero. Performing the long division, we get:
x² - xy + y²
x + y | x³ + 0x² + 0xy + y³
- (x³ + x²y)
----------------
-x²y + 0xy + y³
-(-x²y - xy²)
----------------
xy² + y³
-(xy² + y³)
-------------
0
The remainder is zero, confirming that (x + y) is indeed a factor. The quotient, x² - xy + y², is the other factor.
Proof through Expansion
Alternatively, we can verify the factorization by expanding (x + y)(x² - xy + y²):
(x + y)(x² - xy + y²) = x(x² - xy + y²) + y(x² - xy + y²) = x³ - x²y + xy² + x²y - xy² + y³ = x³ + y³
This confirms our factorization.
Geometric Interpretation of x³ + y³
The sum of cubes has a fascinating geometric interpretation. Imagine two cubes, one with side length x and the other with side length y. The sum of their volumes, x³ and y³, represents the total volume. The factorization (x + y)(x² - xy + y²) can be visualized as the volume of a larger rectangular prism. However, understanding the geometric representation of (x² - xy + y²) requires a more nuanced approach, involving the concepts of volume decomposition and manipulation. While a simple geometric representation for the entire factorization is difficult to directly visualize, the individual components provide insightful geometric meaning in their own right.
Applications of the Sum of Cubes Factorization
The factorization of x³ + y³ isn't just a theoretical curiosity; it has practical applications across various mathematical domains:
-
Solving Cubic Equations: The sum of cubes factorization can be instrumental in solving certain types of cubic equations. By cleverly manipulating the equation to fit the form x³ + y³ = 0, we can use the factorization to find solutions.
-
Calculus: In calculus, the sum of cubes factorization can simplify complex integrals involving cubic expressions. By factoring the integrand, we can often transform a seemingly intractable integral into something easily solvable.
-
Number Theory: The factorization plays a role in number theory, particularly in exploring properties of integers and their relationships. Investigating sums of cubes of integers leads to fascinating insights into number patterns and divisibility rules.
-
Abstract Algebra: In abstract algebra, the sum of cubes factorization helps in understanding polynomial rings and their ideal structures. The factorization provides a valuable tool for analyzing polynomial equations within these abstract algebraic systems.
-
Engineering and Physics: While not as direct as the mathematical applications, the principles underlying the factorization of cubes can find application in problems related to volume calculations, modeling physical phenomena involving cubic relationships, or solving equations arising in engineering designs.
Solving Equations using the Sum of Cubes Factorization
Let's examine a practical example of using the sum of cubes factorization to solve an equation:
Example: Solve the equation x³ + 8 = 0.
First, we rewrite the equation in the form of the sum of cubes:
x³ + 2³ = 0
Now, we apply the factorization:
(x + 2)(x² - 2x + 4) = 0
This equation is satisfied if either (x + 2) = 0 or (x² - 2x + 4) = 0.
Solving (x + 2) = 0 gives us x = -2.
Solving (x² - 2x + 4) = 0 requires the quadratic formula:
x = [2 ± √(4 - 4 * 1 * 4)] / 2 = [2 ± √(-12)] / 2 = 1 ± i√3
Therefore, the solutions to the equation x³ + 8 = 0 are x = -2, x = 1 + i√3, and x = 1 - i√3. This example demonstrates how the factorization allows us to find both real and complex solutions to cubic equations.
Advanced Concepts and Extensions
While we've primarily focused on the basic factorization of x³ + y³, several advanced concepts build upon this foundation:
-
Sum of Higher Powers: The concept of factoring the sum of cubes extends to higher powers, although the factorizations become more complex. For example, the sum of fifth powers, x⁵ + y⁵, also has a factorable form.
-
Difference of Cubes: As previously mentioned, the difference of cubes, x³ - y³, factors differently: (x - y)(x² + xy + y²). Understanding the nuances between the sum and difference of cubes is crucial for effective factorization.
-
Complex Numbers: The solutions to cubic equations involving sums of cubes frequently involve complex numbers, highlighting the interconnectedness between real and complex number systems.
Frequently Asked Questions (FAQ)
Q: What is the difference between x³ + y³ and x³ - y³?
A: The key difference lies in their factorizations. x³ + y³ factors as (x + y)(x² - xy + y²), while x³ - y³ factors as (x - y)(x² + xy + y²). The signs within the quadratic factor are reversed.
Q: Can I use the sum of cubes factorization for any cubic equation?
A: Not all cubic equations can be directly factored using the sum of cubes formula. The equation must be expressible in the form of a sum of two perfect cubes. However, algebraic manipulation can sometimes transform equations into a suitable form.
Q: Are there any geometric interpretations beyond the basic cube volumes?
A: While a direct geometric interpretation of the entire factorization (x + y)(x² - xy + y²) is challenging, the individual factors have clear geometric meaning (the sum of volumes for (x+y), and the other being more complex to directly visualize, but still fundamentally representing a volume). Advanced geometric approaches using volume decomposition and manipulation can offer further insights.
Q: What are some real-world applications beyond mathematics?
A: Although direct applications are primarily within mathematics and its related fields, the underlying concepts and principles of cubic relationships and factorization can inform solutions in fields like engineering or physics where cubic equations arise.
Conclusion
The seemingly simple expression x³ + y³ harbors a depth and significance that extend far beyond its initial appearance. Understanding its factorization, geometric interpretations, and applications allows for a more profound grasp of algebraic manipulation, equation solving, and the interconnectedness of various mathematical disciplines. From solving cubic equations to exploring advanced algebraic concepts, the sum of cubes provides a fertile ground for mathematical exploration and discovery. This exploration has shown us that even seemingly basic mathematical concepts can hold a wealth of complexity and beauty, urging us to further investigate and appreciate the elegance inherent within mathematics. Remember that continued practice and exploration will deepen your understanding and allow you to confidently apply these concepts to diverse mathematical problems.
Latest Posts
Latest Posts
-
71 Fahrenheit To C
Sep 18, 2025
-
1 9 X 180
Sep 18, 2025
-
How Do Lions Mate
Sep 18, 2025
-
50 Percent Of 40
Sep 18, 2025
-
200 Micrograms To Mg
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X 3 Y 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.