110 Divided By 5
renascent
Sep 24, 2025 · 6 min read
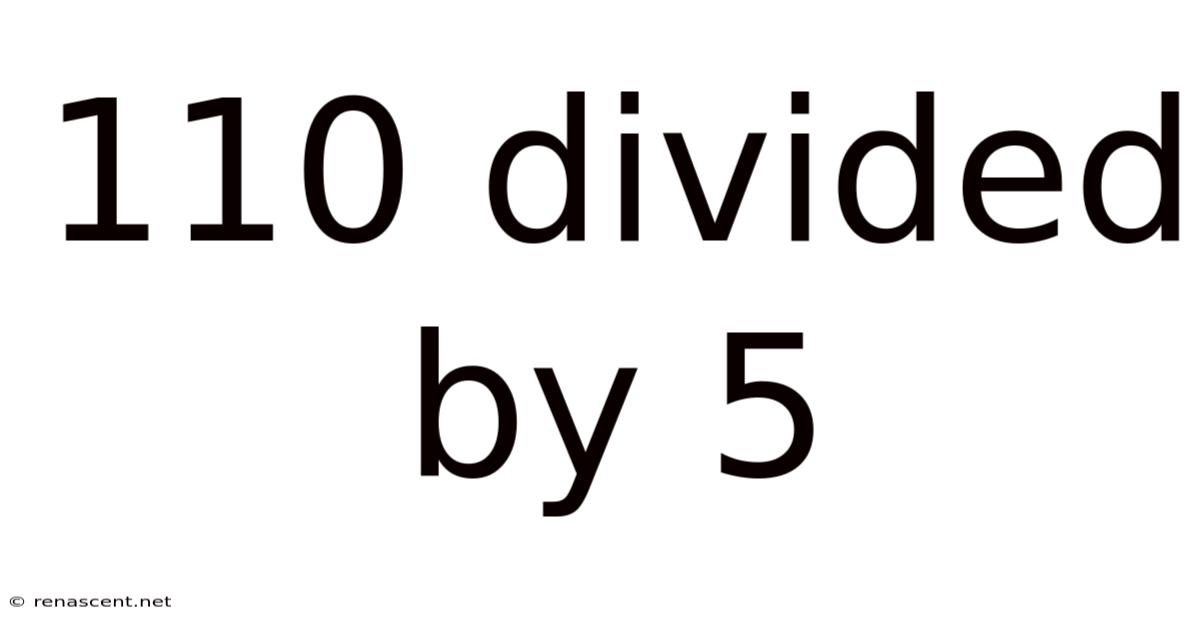
Table of Contents
Unpacking 110 Divided by 5: A Deep Dive into Division
Dividing 110 by 5 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation offers a rich opportunity to explore fundamental mathematical concepts, delve into different approaches to problem-solving, and even touch upon the practical applications of division in everyday life. This article will take you on a journey beyond the simple answer, exploring the "why" behind the calculation and unveiling the underlying mathematical principles.
Introduction: More Than Just an Answer
The question, "What is 110 divided by 5?" is essentially asking how many times 5 fits into 110. The answer, of course, is 22. But understanding how we arrive at this answer is crucial for grasping the broader concept of division and its significance in mathematics and beyond. This article will not only provide the solution but will also explore various methods to solve this problem, examine the underlying mathematical principles, and discuss the real-world applications of division. We'll also address common misconceptions and frequently asked questions. By the end, you'll have a much deeper understanding of division and its importance, moving beyond the simple act of finding the quotient.
Method 1: Long Division – A Classic Approach
Long division is a traditional method taught in schools to solve division problems, especially those involving larger numbers. Let's break down how to solve 110 ÷ 5 using this method:
-
Set up the problem: Write 110 inside the long division symbol (÷) and 5 outside.
5 | 110 -
Divide the tens digit: How many times does 5 go into 1? It doesn't, so we move to the next digit. How many times does 5 go into 11? It goes twice (5 x 2 = 10). Write the '2' above the '1' in 110.
2 5 | 110 -
Subtract and bring down: Subtract 10 from 11, leaving 1. Bring down the next digit, 0, to make 10.
2 5 | 110 -10 10 -
Divide the ones digit: How many times does 5 go into 10? It goes twice (5 x 2 = 10). Write the '2' above the '0' in 110.
22 5 | 110 -10 10 -10 0 -
The remainder: There's a remainder of 0, meaning 5 divides 110 evenly.
Therefore, 110 ÷ 5 = 22.
Method 2: Repeated Subtraction – A Conceptual Approach
Repeated subtraction provides a more intuitive understanding of division. It emphasizes the idea of repeatedly taking away groups of 5 from 110 until nothing remains.
- Start with 110.
- Subtract 5: 110 - 5 = 105.
- Subtract 5 again: 105 - 5 = 100.
- Continue subtracting 5 until you reach 0.
You will find that you have subtracted 5 a total of 22 times. This visually reinforces the concept of division as repeated subtraction. While time-consuming for larger numbers, this method is excellent for building a conceptual understanding of division.
Method 3: Using Multiplication – The Inverse Operation
Division and multiplication are inverse operations. This means that if you know the multiplication facts, you can easily solve division problems. Since 5 x 20 = 100 and 5 x 2 = 10, then 5 x 22 = 110. Therefore, 110 ÷ 5 = 22. This method highlights the interconnectedness of arithmetic operations.
Method 4: Breaking Down the Number – A Strategic Approach
We can simplify the problem by breaking down 110 into numbers easily divisible by 5.
110 can be broken down as 100 + 10.
- 100 ÷ 5 = 20
- 10 ÷ 5 = 2
Adding the results together: 20 + 2 = 22.
This method demonstrates a strategic approach to problem-solving by using smaller, more manageable numbers.
The Mathematical Principles Behind Division
The process of dividing 110 by 5 involves several core mathematical concepts:
- Divisor: The number you're dividing by (5 in this case).
- Dividend: The number being divided (110 in this case).
- Quotient: The result of the division (22 in this case).
- Remainder: The amount left over after dividing (0 in this case).
Division is a fundamental arithmetic operation, the inverse of multiplication. It represents the process of equally sharing or grouping a quantity. Understanding these principles is crucial for tackling more complex mathematical problems.
Real-World Applications of Division
Division isn't just an abstract mathematical concept; it's a tool we use in countless real-world situations:
- Sharing: Equally dividing a group of items among individuals. For instance, dividing 110 candies among 5 friends.
- Measurement: Converting units of measurement. For example, converting 110 centimeters to meters (110 cm ÷ 100 cm/m = 1.1 m).
- Rate and Ratio: Calculating speed, price per unit, or proportions. If you travel 110 miles in 5 hours, your average speed is 22 mph (110 miles ÷ 5 hours = 22 mph).
- Averages: Determining the average of a set of numbers.
- Finance: Calculating per-unit costs, splitting bills, or determining investment returns.
Common Misconceptions about Division
- Order of Operations: Division doesn't always come before multiplication. Follow the order of operations (PEMDAS/BODMAS) strictly.
- Dividing by Zero: Dividing any number by zero is undefined. It's a crucial concept to understand.
- Decimal Division: Don't be intimidated by decimals. The principles remain the same.
Frequently Asked Questions (FAQ)
-
What if the remainder is not zero? If the remainder is not zero, it means the divisor doesn't divide the dividend evenly. The remainder is often expressed as a fraction or decimal. For example, if we divide 112 by 5, we get 22 with a remainder of 2, which can be expressed as 22 2/5 or 22.4.
-
Can I use a calculator? Absolutely! Calculators are helpful tools for solving division problems, especially those involving larger numbers or decimals. However, understanding the underlying principles remains crucial.
-
Why is division important? Division is a fundamental skill applied across various fields – from simple everyday tasks to complex scientific calculations. A strong grasp of division builds a solid foundation for more advanced mathematical concepts.
Conclusion: Beyond the Simple Answer
While the answer to 110 divided by 5 is 22, this article has aimed to go beyond the simple solution. We've explored various methods for solving this problem, examined the underlying mathematical principles, and highlighted the real-world applications of division. By understanding the "why" behind the calculation, we gain a far deeper appreciation for this fundamental mathematical operation and its significance in our daily lives. Remember, mathematics is more than just numbers; it's about understanding relationships, patterns, and problem-solving skills that are essential for navigating the world around us. So, the next time you encounter a division problem, remember the journey, not just the destination.
Latest Posts
Latest Posts
-
1 Quarter Of 16
Sep 24, 2025
-
Biggest Baby Ever Born
Sep 24, 2025
-
42 Divided By 4
Sep 24, 2025
-
52 60 As A Percentage
Sep 24, 2025
-
Optimum Temperature For Catalase
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 110 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.