24/40 As A Percent
renascent
Sep 23, 2025 · 5 min read
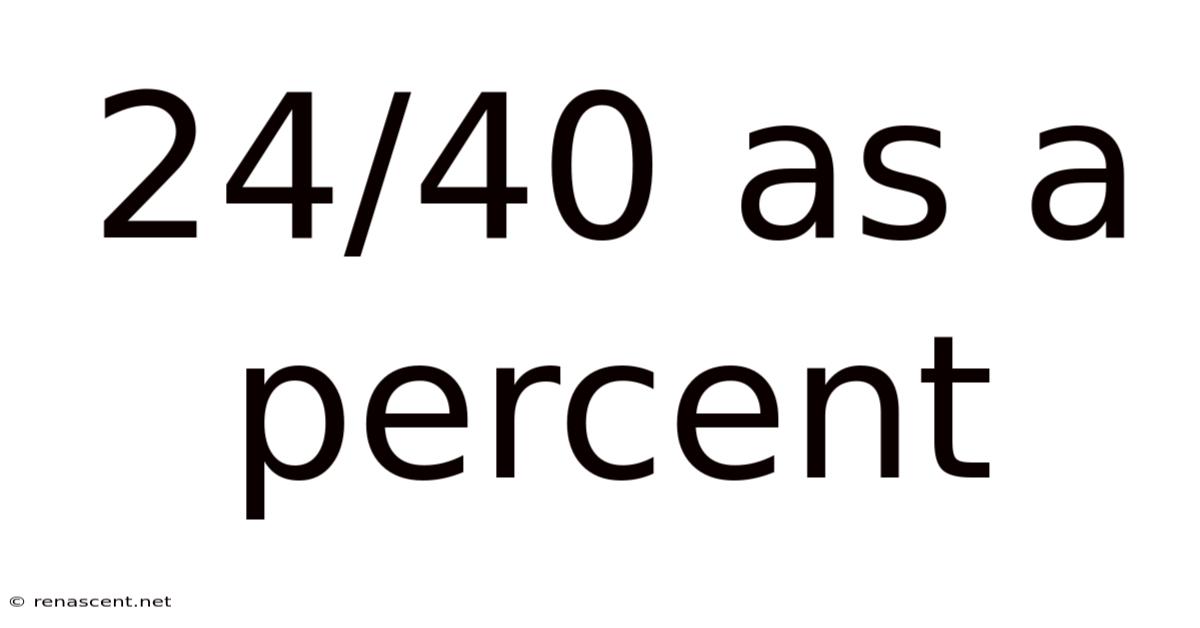
Table of Contents
Understanding 24/40 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of converting the fraction 24/40 into a percentage, explaining the underlying principles and providing practical examples. We'll cover not only the calculation itself but also the broader context of fractions, decimals, and percentages, equipping you with a solid understanding of this crucial mathematical concept.
Introduction: Fractions, Decimals, and Percentages
Before we dive into converting 24/40, let's establish a clear understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fraction: A fraction expresses a part of a whole as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For example, 24/40 means 24 parts out of a total of 40 parts.
-
Decimal: A decimal represents a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). Decimals use a decimal point to separate the whole number from the fractional part.
-
Percentage: A percentage expresses a fraction or decimal as a proportion of 100. The symbol "%" signifies "per hundred." A percentage indicates how many parts out of 100 make up a whole.
These three are interchangeable. You can convert a fraction to a decimal, a decimal to a percentage, and so on. This interconvertibility is extremely useful in various mathematical applications.
Calculating 24/40 as a Percentage: Step-by-Step Guide
There are two primary methods to convert 24/40 to a percentage:
Method 1: Simplifying the Fraction First
This method involves simplifying the fraction to its lowest terms before converting to a percentage. Simplifying a fraction means reducing the numerator and denominator by their greatest common divisor (GCD).
-
Find the GCD of 24 and 40: The GCD of 24 and 40 is 8. This means both numbers are divisible by 8.
-
Simplify the fraction: Divide both the numerator and the denominator by the GCD (8):
24 ÷ 8 = 3 40 ÷ 8 = 5
The simplified fraction is 3/5.
-
Convert the simplified fraction to a decimal: Divide the numerator (3) by the denominator (5):
3 ÷ 5 = 0.6
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%):
0.6 x 100 = 60%
Therefore, 24/40 is equal to 60%.
Method 2: Direct Conversion to Percentage
This method involves directly converting the fraction to a percentage without simplification.
-
Convert the fraction to a decimal: Divide the numerator (24) by the denominator (40):
24 ÷ 40 = 0.6
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%):
0.6 x 100 = 60%
This method yields the same result: 24/40 is equal to 60%. While this method is quicker, simplifying the fraction first (Method 1) can be helpful for understanding the underlying relationship between the numbers and can be particularly useful when dealing with larger or more complex fractions.
Understanding the Result: What does 60% mean?
The result, 60%, signifies that 24 represents 60 parts out of every 100 parts of the whole represented by 40. In simpler terms, if you had 40 apples and you took 24, you would have taken 60% of the apples.
Real-World Applications of Percentage Conversions
The ability to convert fractions to percentages is crucial in many real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates all involve working with percentages.
-
Statistics: Percentages are used to represent data in graphs, charts, and reports, making it easier to understand and visualize information.
-
Everyday Life: Calculating tips, sales tax, and understanding discounts all require an understanding of percentages.
-
Science: Percentages are used to express concentrations, yields, and errors in scientific experiments and data analysis.
Further Exploration: Working with Percentages
Let's explore some related concepts that build upon the understanding of converting fractions to percentages:
-
Calculating the Percentage of a Number: To find a percentage of a number, you multiply the number by the percentage (expressed as a decimal). For example, to find 60% of 80, you would calculate 0.6 x 80 = 48.
-
Finding the Percentage Increase or Decrease: This involves calculating the change in a value and expressing it as a percentage of the original value. The formula is: [(New Value - Old Value) / Old Value] x 100%.
-
Working with Compound Percentages: Compound percentages involve applying a percentage to a value, and then applying another percentage to the resulting value. This is common in financial calculations like compound interest.
Frequently Asked Questions (FAQ)
Q1: Is there a difference between simplifying the fraction first and directly converting to a percentage?
A1: No, the final result will be the same. Simplifying first improves understanding and can be easier with more complex fractions. Direct conversion is quicker for simpler fractions.
Q2: What if the fraction results in a repeating decimal?
A2: If the decimal is repeating, you can either round it to a certain number of decimal places before converting to a percentage or express the percentage using a fraction.
Q3: How can I convert a percentage back to a fraction?
A3: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 60% = 60/100 = 3/5.
Conclusion: Mastering Percentage Conversions
Converting fractions like 24/40 to percentages is a fundamental mathematical skill with wide-ranging applications. By understanding the underlying principles and practicing different methods, you can confidently tackle percentage calculations in various contexts. Remember, the key lies in understanding the relationship between fractions, decimals, and percentages – all different expressions representing parts of a whole. Mastering this skill opens doors to a deeper understanding of numerous mathematical and real-world concepts. This ability enhances problem-solving skills and contributes to a more comprehensive understanding of quantitative data. Consistent practice and a focus on understanding the underlying principles will solidify your mastery of this important skill.
Latest Posts
Latest Posts
-
Pair Factors Of 72
Sep 23, 2025
-
Show Routes In Windows
Sep 23, 2025
-
80 Percent Of 50
Sep 23, 2025
-
68 To A Fraction
Sep 23, 2025
-
Stages Of Skill Acquisition
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 24/40 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.