27/40 As A Percent
renascent
Sep 20, 2025 · 5 min read
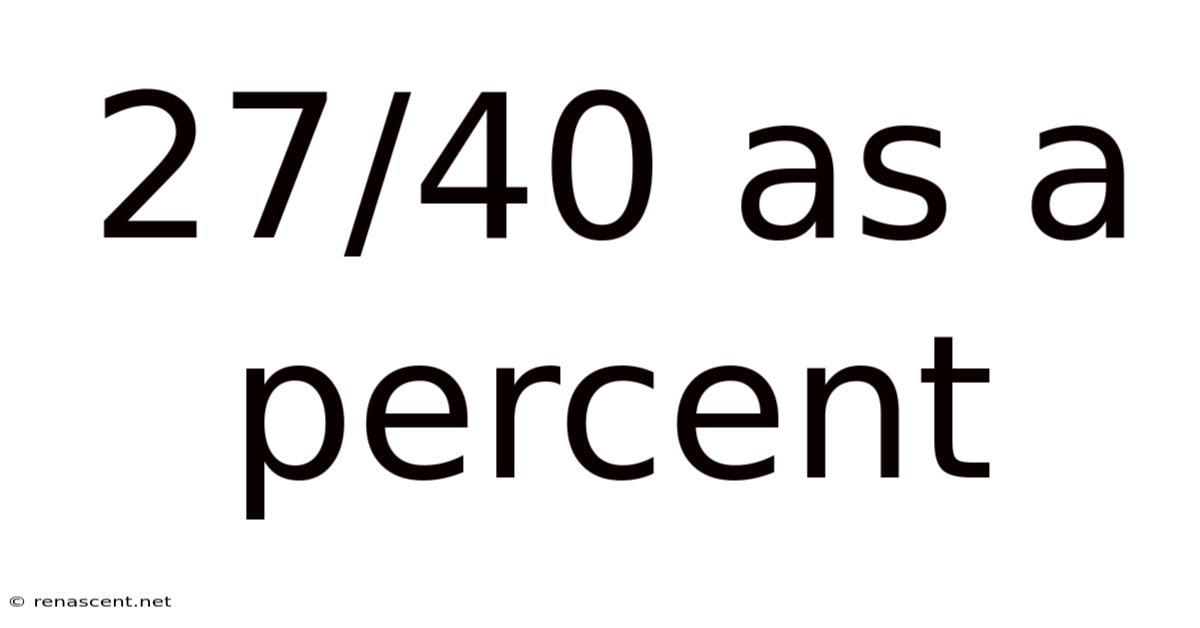
Table of Contents
Decoding 27/40 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics, crucial for various applications from calculating grades to understanding financial data. This article will comprehensively explain how to convert the fraction 27/40 into a percentage, exploring different methods and offering a deeper understanding of the underlying concepts. We'll also delve into the practical implications and applications of this conversion, addressing frequently asked questions along the way.
Introduction: Understanding Fractions and Percentages
Before diving into the conversion of 27/40, let's quickly recap the basics of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For instance, in the fraction 27/40, 27 is the numerator and 40 is the denominator. This means we're considering 27 parts out of a total of 40 parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of 100 parts. So, 50% means 50 out of 100, which is equivalent to ½ or 0.5. Converting fractions to percentages essentially involves expressing the fraction as an equivalent fraction with a denominator of 100.
Method 1: The Direct Conversion Method
The most straightforward method to convert 27/40 to a percentage is to use the following formula:
(Numerator / Denominator) * 100%
Substituting the values from our fraction:
(27 / 40) * 100% = 0.675 * 100% = 67.5%
Therefore, 27/40 is equal to 67.5%.
This method is simple and efficient, particularly when dealing with fractions that can be easily converted to decimal form. However, it might not always be the most intuitive approach, especially for those less comfortable with decimal calculations.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another way to convert 27/40 to a percentage is to find an equivalent fraction with a denominator of 100. This method relies on the principle that multiplying or dividing both the numerator and the denominator of a fraction by the same number doesn't change its value.
To achieve a denominator of 100, we need to determine what number, when multiplied by 40, equals 100. This can be found by solving the equation:
40 * x = 100
Solving for x, we get x = 100/40 = 2.5
Now, we multiply both the numerator and denominator of 27/40 by 2.5:
(27 * 2.5) / (40 * 2.5) = 67.5 / 100
This equivalent fraction, 67.5/100, directly represents 67.5%. This method provides a clearer visual representation of the percentage, directly linking it to the concept of "parts per hundred".
Method 3: Using Decimal Representation
A third approach involves first converting the fraction to a decimal and then multiplying by 100%.
To convert 27/40 to a decimal, we simply divide the numerator by the denominator:
27 ÷ 40 = 0.675
Now, multiplying this decimal by 100% gives us the percentage:
0.675 * 100% = 67.5%
This method is particularly useful when dealing with fractions that don't easily lend themselves to finding an equivalent fraction with a denominator of 100. It highlights the strong connection between decimals and percentages.
Understanding the Result: 67.5%
We've established through three different methods that 27/40 is equal to 67.5%. This means that 27 represents 67.5% of 40. In simpler terms, if you divide 40 into 100 equal parts, 27 would occupy 67.5 of those parts. This understanding is crucial for interpreting the result within different contexts.
Practical Applications of Percentage Conversion
The ability to convert fractions to percentages has widespread applications across various fields:
-
Academic Performance: Calculating grades and assessing academic progress often involves converting fractional scores into percentages. A score of 27 out of 40 on a test translates to a 67.5% grade.
-
Financial Calculations: Percentages are crucial in finance, from calculating interest rates and discounts to analyzing investment returns. Understanding percentage changes is vital for interpreting financial data effectively.
-
Data Analysis: Expressing data as percentages simplifies comparisons and facilitates a clear understanding of proportions within datasets.
-
Everyday Life: Many everyday situations involve percentages, from calculating sales tax and tips to understanding statistics in news reports.
Frequently Asked Questions (FAQ)
-
Q: Can I round off 67.5% to 68%?
- A: Whether to round off depends on the context. In some situations, precision is crucial, and rounding off would be inappropriate. In others, rounding to 68% might be acceptable for simplification.
-
Q: How can I convert other fractions to percentages?
- A: You can use any of the three methods outlined above. The choice depends on your comfort level with decimals and your preference for visual representation.
-
Q: What if the fraction has a larger denominator?
- A: The same principles apply. You can use the direct conversion method, find an equivalent fraction with a denominator of 100 (though this might be more challenging), or convert to a decimal first.
-
Q: Why is understanding percentage conversion important?
- A: It allows you to easily compare and interpret different proportions, making data analysis and decision-making more efficient. It’s a fundamental skill with broad applications in various aspects of life.
Conclusion: Mastering Percentage Conversions
Converting fractions like 27/40 to percentages is a valuable skill that transcends the boundaries of the classroom. Understanding the different methods – direct conversion, finding an equivalent fraction, and using decimal representation – empowers you to approach such conversions with confidence. By mastering this skill, you enhance your ability to analyze data, interpret information, and solve problems across various disciplines. Remember, the key lies in understanding the underlying principles and choosing the method that best suits your needs and comfort level. The ability to effortlessly convert fractions to percentages is a cornerstone of mathematical literacy and practical problem-solving.
Latest Posts
Latest Posts
-
11 15 2 5
Sep 21, 2025
-
12 16 In Percentage
Sep 21, 2025
-
26 Squared 24 Squared
Sep 21, 2025
-
35 Divided By 2
Sep 21, 2025
-
165 Kilos In Pounds
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 27/40 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.