39/60 As A Percentage
renascent
Sep 20, 2025 · 5 min read
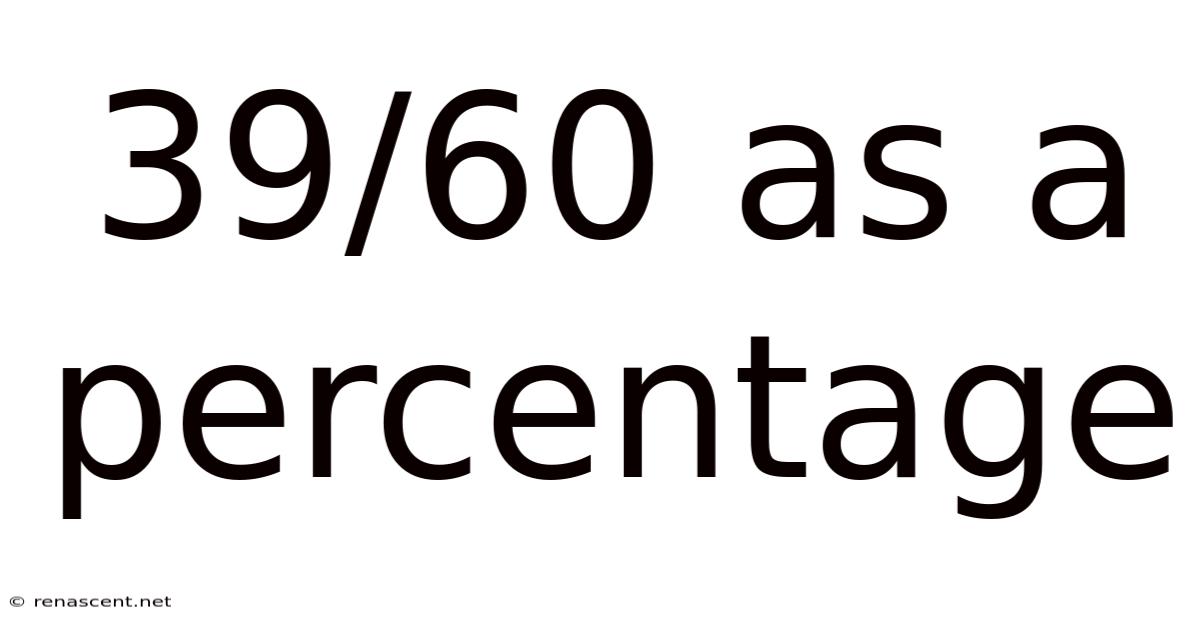
Table of Contents
39/60 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications spanning various fields, from finance and budgeting to scientific calculations and data analysis. This comprehensive guide will explore how to convert the fraction 39/60 into a percentage, providing a step-by-step process, explaining the underlying mathematical principles, and addressing common questions. We'll delve into the practical applications and explore the concept in detail, ensuring a thorough understanding for learners of all levels.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before diving into the specific conversion of 39/60, let's establish the foundational relationships between fractions, decimals, and percentages. They are different ways of representing parts of a whole.
-
Fractions: Express a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 39/60 represents 39 parts out of a total of 60 parts.
-
Decimals: Represent a part of a whole using a base-ten system. The decimal point separates the whole number part from the fractional part.
-
Percentages: Represent a part of a whole as a fraction of 100. The symbol "%" denotes "per hundred." For example, 65% means 65 out of 100.
These three representations are interchangeable, meaning you can convert one form into another without changing the underlying value. This conversion is crucial for various applications, ensuring consistent interpretation and comparison of data.
Step-by-Step Conversion of 39/60 to a Percentage
The conversion of 39/60 to a percentage involves two primary steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, you simply divide the numerator by the denominator:
39 ÷ 60 = 0.65
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.65 x 100 = 65%
Therefore, 39/60 is equal to 65%.
Simplifying the Fraction Before Conversion (Optional but Recommended)
While the above method is perfectly valid, simplifying the fraction before conversion can make the calculation easier. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 39 and 60 is 3. Dividing both the numerator and the denominator by 3, we get:
39 ÷ 3 = 13 60 ÷ 3 = 20
This simplifies the fraction to 13/20. Now, we can convert this simplified fraction to a decimal:
13 ÷ 20 = 0.65
Converting the decimal to a percentage:
0.65 x 100 = 65%
As you can see, we arrive at the same result, 65%, regardless of whether we simplify the fraction first. However, simplifying often leads to simpler calculations, particularly with larger fractions.
Understanding the Mathematical Principles
The conversion process relies on the fundamental principle that percentages are always expressed as a fraction of 100. When we multiply a decimal by 100, we are essentially scaling the decimal to represent parts of 100, which is the definition of a percentage.
The division step (converting the fraction to a decimal) finds the equivalent decimal value representing the proportion of the whole. This decimal value then provides a direct representation of the fraction's proportion relative to the whole, easily convertible to a percentage.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages has numerous real-world applications across various disciplines:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates.
-
Statistics: Representing data in a visually understandable manner, like in pie charts or bar graphs.
-
Science: Expressing experimental results, such as the percentage of successful trials or the concentration of a solution.
-
Everyday Life: Calculating tips, understanding sales, determining the percentage of completion of a task.
-
Education: Evaluating test scores, understanding class performance, and assessing progress.
Beyond the Basics: Dealing with More Complex Fractions
While 39/60 is a relatively straightforward fraction, the principles discussed above apply to more complex fractions as well. For fractions with larger numbers or decimals in the numerator or denominator, a calculator might be helpful for the division step. However, the underlying process remains the same: divide the numerator by the denominator to get the decimal equivalent, and then multiply by 100 to obtain the percentage.
Frequently Asked Questions (FAQ)
Q1: What if the fraction is an improper fraction (where the numerator is larger than the denominator)?
A1: Even with improper fractions, the process remains the same. Divide the numerator by the denominator; the resulting decimal will be greater than 1. Multiplying this decimal by 100 will give you a percentage greater than 100%.
Q2: Can I use a calculator to convert fractions to percentages?
A2: Yes, most calculators have built-in functions to handle fraction-to-decimal and decimal-to-percentage conversions. Simply input the fraction (often as a division problem) and let the calculator perform the calculations.
Q3: Are there any shortcuts for converting specific fractions to percentages?
A3: While no universal shortcuts exist, recognizing common fractions and their percentage equivalents (e.g., 1/2 = 50%, 1/4 = 25%, 3/4 = 75%) can sometimes speed up the process. These common equivalents often serve as a basis for calculating other fractions' percentages.
Q4: Why is understanding percentage conversions important?
A4: Percentages provide a standardized way to compare different proportions or fractions. They offer a clear and easily interpretable representation of data, crucial for making informed decisions in various contexts. They allow for easier comparisons between different data sets which might be represented in various forms.
Conclusion: Mastering the Art of Percentage Conversion
Converting fractions to percentages is a fundamental skill with widespread practical applications. This guide has provided a detailed walkthrough of the process, clarifying the mathematical principles involved and addressing common questions. By understanding the steps involved and the underlying concepts, you can confidently tackle various percentage conversion problems, whether dealing with simple fractions like 39/60 or more complex ones. The ability to seamlessly move between fractions, decimals, and percentages significantly enhances your mathematical fluency and problem-solving capabilities across diverse fields. Remember, practice is key to mastering this valuable skill. Work through several examples, and soon, you'll be converting fractions to percentages with ease and confidence.
Latest Posts
Latest Posts
-
40 Divided By 10
Sep 21, 2025
-
11 15 2 5
Sep 21, 2025
-
12 16 In Percentage
Sep 21, 2025
-
26 Squared 24 Squared
Sep 21, 2025
-
35 Divided By 2
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 39/60 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.